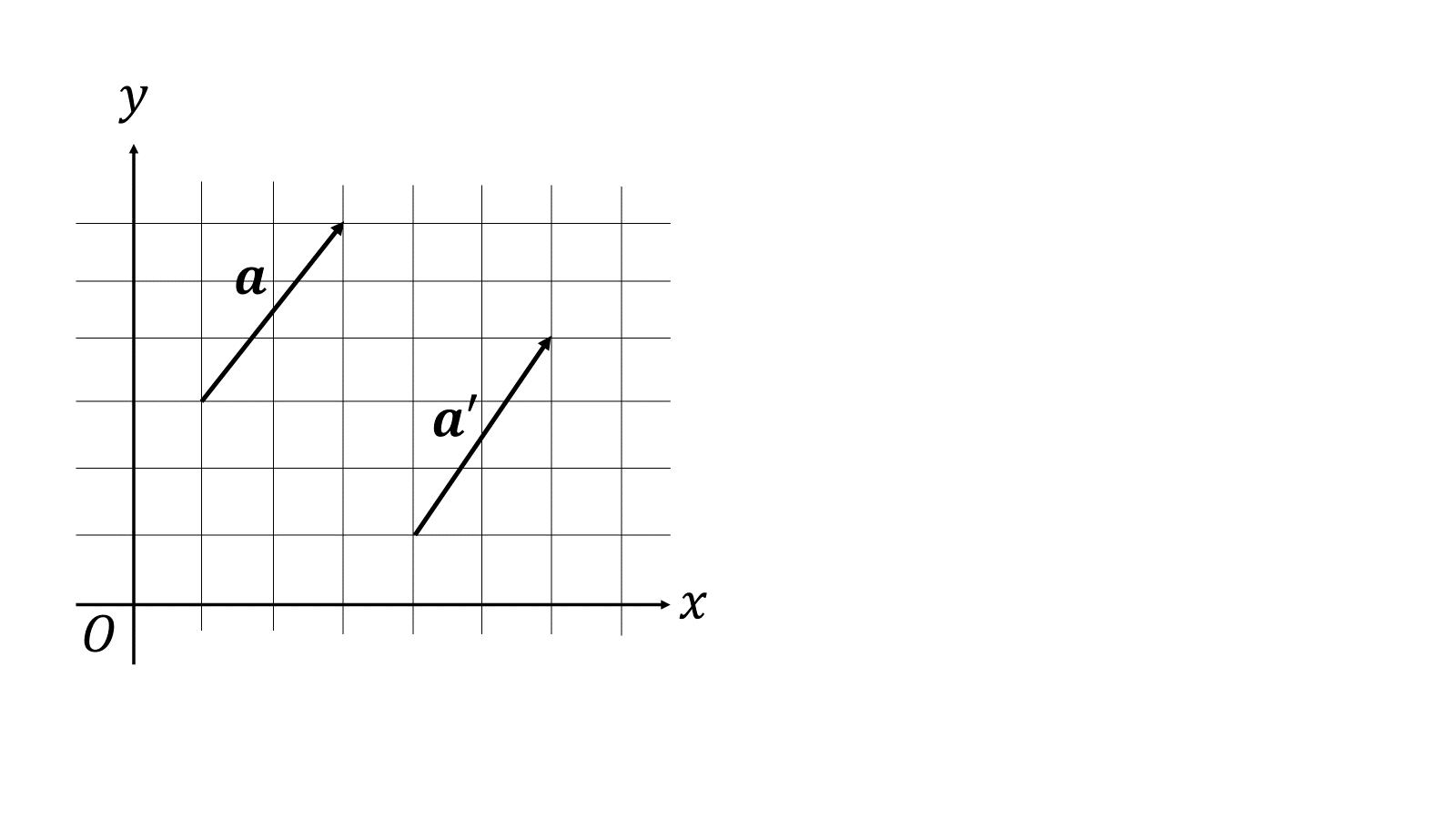今回から一般相対性理論について説明していこう。ニュートン力学では、万有引力の法則により、質量をもつ物体同士に相互作用がはたらくと考えた。一般相対性理論では、質量をもつ物体が時間、空間を歪めると考える。まずは、理解しやすいように２次元で話をする。

/*　\(ℝ^2\)ユークリッド空間(\(x,y\)軸が直交した平面)のイメージ

　\(ℝ^2\)のベクトル\(\boldsymbol{a}\)は基底ベクトルを用いで、 \[\boldsymbol{a}=a^1\boldsymbol{e}_1+a^2\boldsymbol{e}_2\] と表せる。

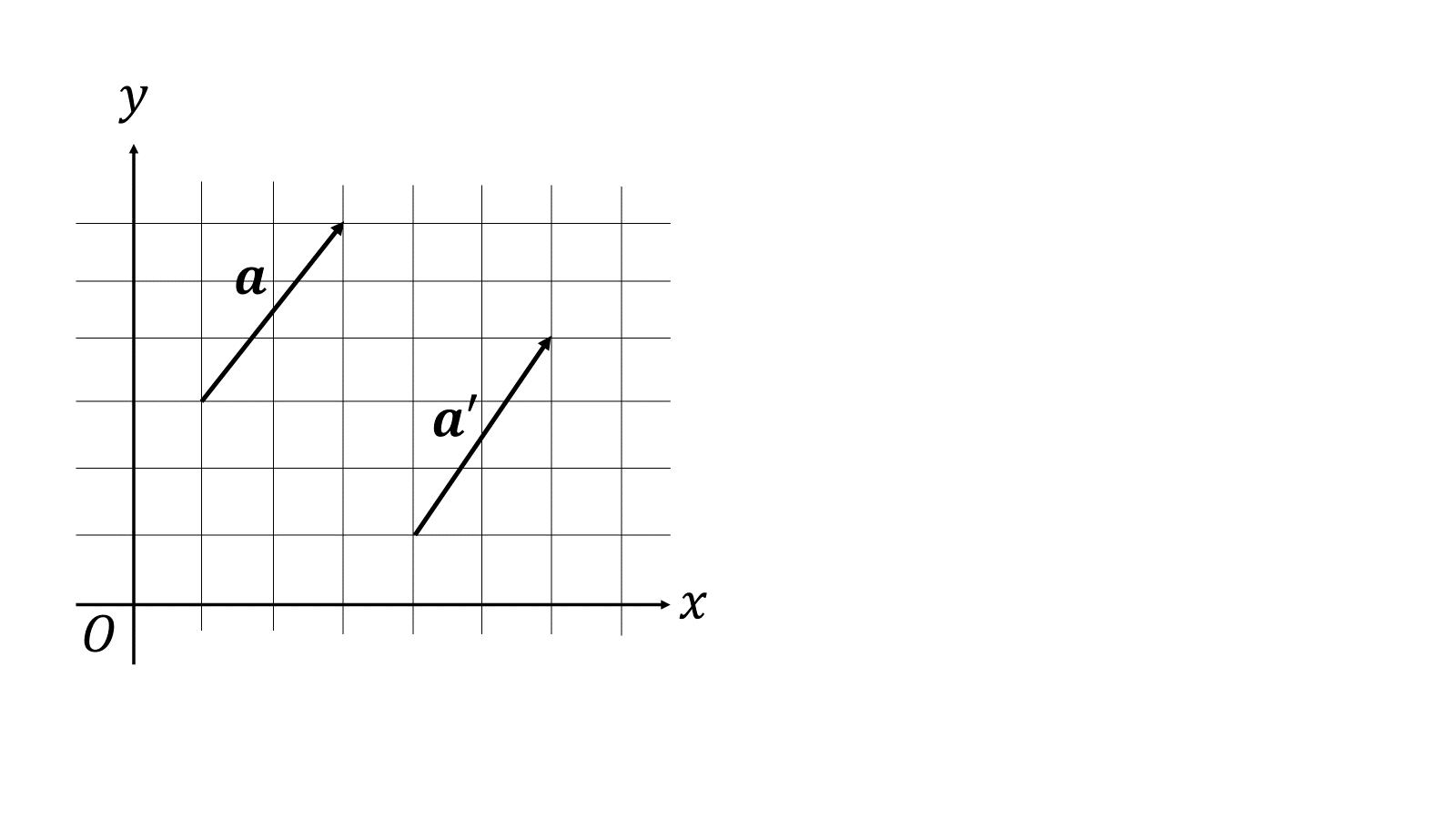
ベクトル\(\boldsymbol{a}\)と\(\boldsymbol{a}'\)の向き、大きさが同じなら、 \[\boldsymbol{a}=\boldsymbol{a}'\] である。ベクトルの内積は、 \[\boldsymbol{a}\cdot\boldsymbol{b}=a^1b^1+a^2b^2\] である。 \[\delta_{ij}= \begin{cases}1 & i=j\\0 &i\neq j\end{cases}\] このようなテンソルを用いると、内積は \[\boldsymbol{a}\cdot\boldsymbol{b}=a^ib^i=\delta_{ij}a^ib^{j}\] のように表せる。ベクトル場\(\boldsymbol{A}(\boldsymbol{x}\))(電場や保存力など、位置の関数になっているベクトル)は、 \[\boldsymbol{A}(\boldsymbol{x})=A^1(x,y)\boldsymbol{e}_1+A^2(x,y)\boldsymbol{e}_2\] のように表せる。ベクトル場の\(x^i\)(\(x\)または\(y\))方向の偏微分は、 \[\frac{\partial \boldsymbol{A}}{\partial x^i}=\frac{\partial A^1}{\partial x^i}\boldsymbol{e}_1+\frac{\partial A^2}{\partial x^i}\boldsymbol{e}_2\tag{1}\] ここまでは大丈夫だと思う。

終わり*/

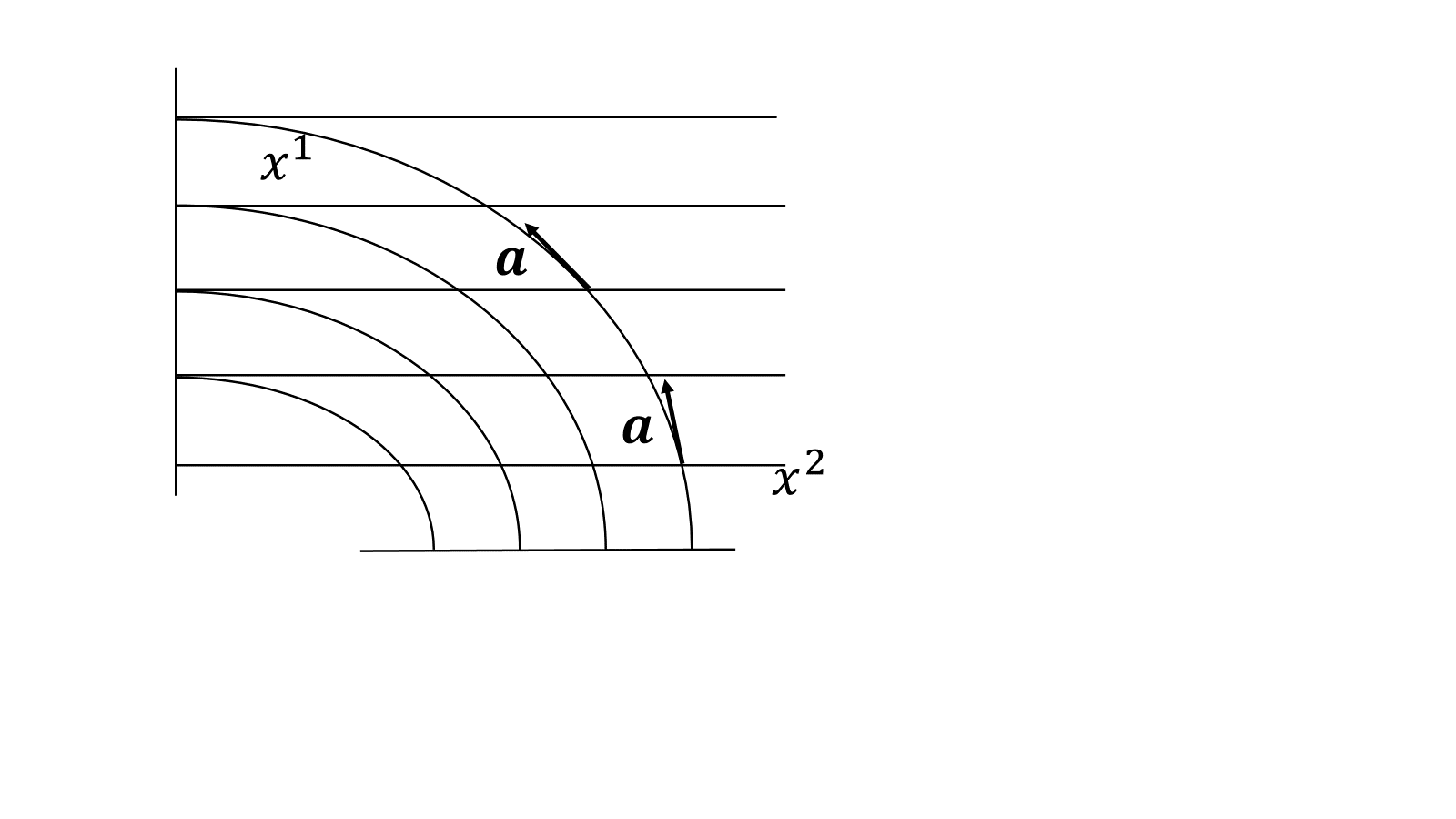
　図のように、\(x^1\)軸が曲がっている平面について、\(x^1\)軸正の方向に\(\boldsymbol{a}\)だけ進むことを考える。同じく\(\boldsymbol{a}\)並進したはずなのに、空間のどこにいるかでベクトル\(\boldsymbol{a}\)が別のベクトルになっている。一定のベクトルでも空間の位置に依存した量になっている。

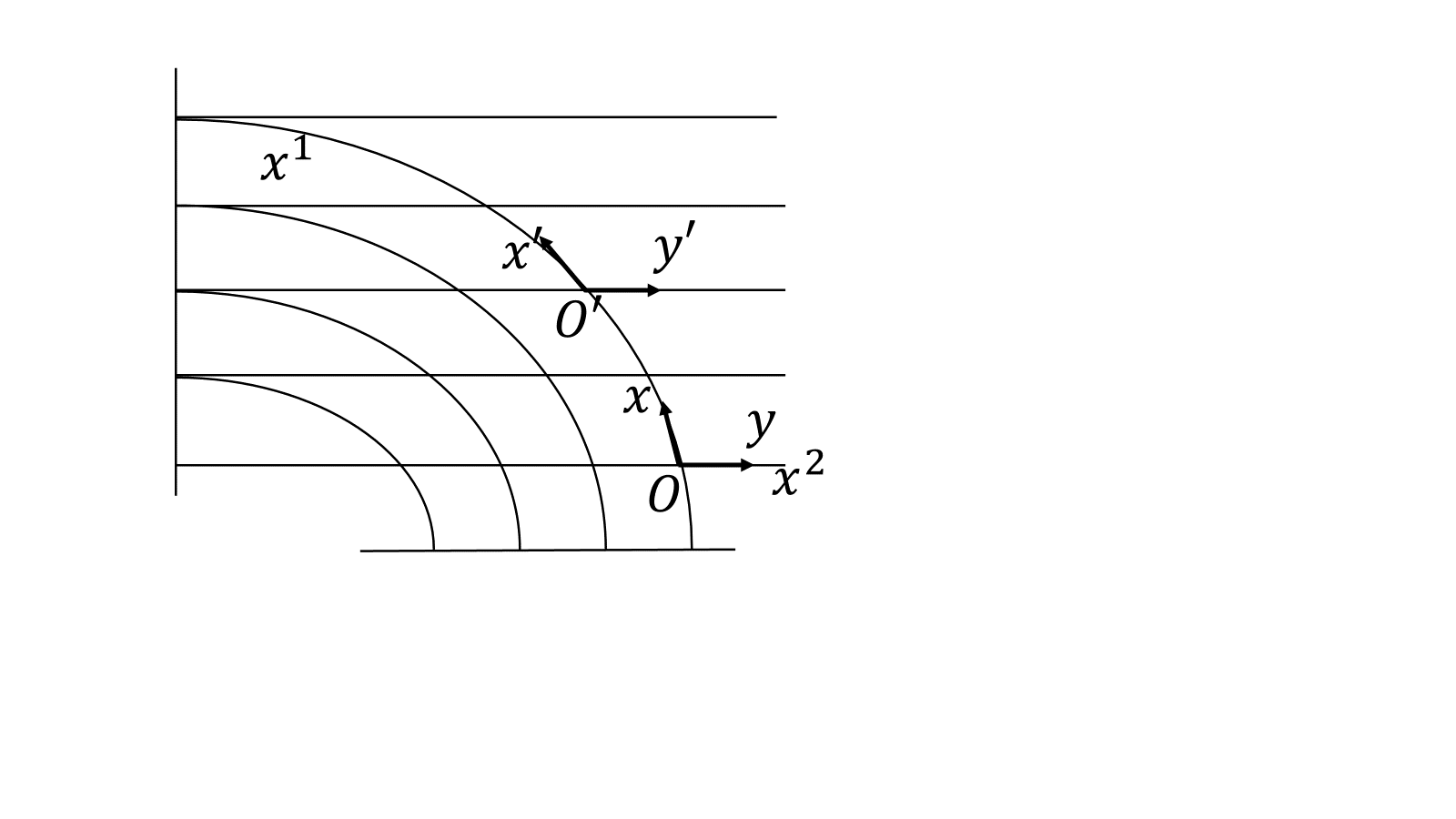
　そこで、このように考えよう。空間の任意の点\(P,P'\)について、その点\(P,P'\)周り近傍のみで使える局所座標\(O(x,y),O'(x',y')\)というものを考えると、 \[\boldsymbol{a}=a^1(P)\boldsymbol{e}_1(P)+a^2(P)\boldsymbol{e}_2(P)\] \[\boldsymbol{a}'=a'^1(P')\boldsymbol{e}'_1(P')+a'^2(P')\boldsymbol{e}'_2(P')\] のように表記することにする。ただし、基底ベクトルも成分も空間の位置によって変化する。歪んだ平面上のある点\(P\)での基底ベクトル\(\boldsymbol{e}_1,\boldsymbol{e}_2\)を使って計量テンソルを \[g_{ij}(P):=\boldsymbol{e}_i(P)\cdot\boldsymbol{e}_j(P)\] のように定義することで、 点\(P\)で、ベクトルの内積を \[\boldsymbol{a}\cdot\boldsymbol{b}=g_{ij}(P)a^i(P)b^j(P)\] と表せる。 このような空間でベクトル場\(\boldsymbol{A}(\boldsymbol{x})\)を \[\boldsymbol{A}(\boldsymbol{x})=A^1(x^1,x^2)\boldsymbol{e}_1(x^1,x^2)+A^2(x^1,x^2)\boldsymbol{e}_2(x^1,x^2)\] のように基底ベクトルも位置の関数になる。直交座標系では、(1)のように微分できたが、歪んだ空間では、 \[\frac{\partial\boldsymbol{A}}{\partial x^i}=\frac{\partial A^1}{\partial x^i}\boldsymbol{e}_1+A^1\frac{\partial\boldsymbol{e}_1}{\partial x^i}+\frac{\partial A^2}{\partial x^i}\boldsymbol{e}_2+A^2\frac{\partial\boldsymbol{e}_2}{\partial x^i}\] のように基底ベクトルも微分しなければならない。(1)式のように、\(\partial_i\boldsymbol{A}=\sim\boldsymbol{e}_1+\sim\boldsymbol{e}_2\)のような形(成分表示)で書きたい！そこでクリストッフェルの記号というものが便利である。

＊＊クリストッフェルの記号＊＊

\[\frac{\partial \boldsymbol{e}_{\mu}}{\partial x^\nu}:=\Gamma_{\ \mu\nu}^{\xi}\boldsymbol{e}_{\xi}\]

上記は縮約をした定義である。クリストッフェルの記号\(\Gamma_{\ \mu\nu}^{\xi}\)は、\(\mu\)方向の基底ベクトルを、\(\nu\)方向に微分したベクトルの\(\xi\)方向の基底ベクトルの係数を教えてくれる。計算は難しい(できなくないが、計量が必要になる。)ので、とりあえずクリストッフェルの記号を使って計算したことにする。ということである。例えば\(\boldsymbol{e}_1\)の\(x^2\)方向の微分は \[\frac{\partial\boldsymbol{e}_1}{\partial x^2}=\Gamma_{\ 12}^{1}\boldsymbol{e}_1+\Gamma_{\ 12}^{2}\boldsymbol{e}_2\] のように計算したことにできるので、 \[\frac{\partial\boldsymbol{A}}{\partial x^i}=\frac{\partial A^1}{\partial x^i}\boldsymbol{e}_1+A^1\frac{\partial\boldsymbol{e}_1}{\partial x^i}+\frac{\partial A^2}{\partial x^i}\boldsymbol{e}_2+A^2\frac{\partial\boldsymbol{e}_2}{\partial x^i}\] \[=\frac{\partial A^1}{\partial x^i}\boldsymbol{e}_1+A^1\Gamma_{\ 1i}^{1}\boldsymbol{e}_1+A^1\Gamma_{\ 1i}^{2}\boldsymbol{e}_2\] \[+\frac{\partial A^2}{\partial x^i}\boldsymbol{e}_2+A^1\Gamma_{\ 2i}^{1}\boldsymbol{e}_1+A^1\Gamma_{\ 2i}^{2}\boldsymbol{e}_2\] ごちゃごちゃなので、\(\partial/\partial x^i=\partial_i\)とかきます。すいません。 \[=\left(\partial_iA^1+A^1\Gamma_{\ 1i}^{1}+A^2\Gamma_{\ 2i}^{1}\right)\boldsymbol{e}_1\] \[+\left(\partial_iA^2+A^1\Gamma_{\ 1i}^{2}+A^2\Gamma_{\ 2i}^{2}\right)\boldsymbol{e}_2\] クリストッフェルの記号について、アインシュタインの縮約記法を使うと、 \[\frac{\partial\boldsymbol{A}}{\partial x^i}=(\partial_iA^1+A^\alpha\Gamma_{\ \alpha i}^{1})\boldsymbol{e}_1+(\partial_iA^2+A^\alpha\Gamma_{\ \alpha i}^{2})\boldsymbol{e}_2\] 更に基底ベクトルも縮約を取ると、 \[\partial_i\boldsymbol{A}=(\partial_iA^{\mu}+A^\alpha\Gamma_{\ \alpha i}^{\mu})\boldsymbol{e}_{\mu}\] 直交座標では\(\partial_i\boldsymbol{A}\)の\(\mu\)成分は\(\partial_iA^{\mu}\)であるが、歪んだ空間ではこれと区別して、\(A^{\mu}_{\ ;i},\ \nabla_iA^{\mu}\)などと書いたりする。

＊＊共変微分＊＊

非ユークリッド空間(歪んだ空間)で、ベクトル場\(\boldsymbol{A}\)の\(x^i\)方向微分の\(\mu\)成分は次のように表せる。 \[A^{\mu}_{\ ;i}:=\partial_iA^{\mu}+\Gamma_{\ \nu i}^{\mu}A^{\nu}\]

　で、結局クリストッフェルの記号ってなんだよ。ってなると思う。計量テンソル\(g_{\mu\nu}\)を使って表すとこができるが、そのために行列と、双対基底について学ぶ必要がある。先は長い。

/*　蛇足

　共変微分は相対性理論に応用するために紹介したが４次元でも同じ結果が得られる。 \[\partial_i(A^{\mu}\boldsymbol{e}_\mu)\] \[=\partial_i(A^0\boldsymbol{e}_0+A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2+A^3\boldsymbol{e}_3)\] \[=\partial_iA^0\boldsymbol{e}_0+\partial_iA^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2+\partial_iA^3\boldsymbol{e}_3\] \[+A^0\frac{\partial\boldsymbol{e}_0}{\partial x^i}+A^1\frac{\partial\boldsymbol{e}_1}{\partial x^i}+A^2\frac{\partial\boldsymbol{e}_2}{\partial x^i}+A^3\frac{\partial\boldsymbol{e}_3}{\partial x^i}\] クリストッフェルの記号を使うと、 \[=\partial_iA^0\boldsymbol{e}_0+\partial_iA^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2+\partial_iA^3\boldsymbol{e}_3\] \[+A^0(\Gamma_{\ 0i}^0\boldsymbol{e}_0+\Gamma_{\ 0i}^1\boldsymbol{e}_1+\Gamma_{\ 0i}^2\boldsymbol{e}_2+\Gamma_{\ 0i}^3\boldsymbol{e}_3)\] \[+A^1(\Gamma_{\ 1i}^0\boldsymbol{e}_0+\Gamma_{\ 1i}^1\boldsymbol{e}_1+\Gamma_{\ 1i}^2\boldsymbol{e}_2+\Gamma_{\ 1i}^3\boldsymbol{e}_3)\] \[\cdots\] \[+A^3(\Gamma_{\ 3i}^0\boldsymbol{e}_0+\Gamma_{\ 3i}^1\boldsymbol{e}_1+\Gamma_{\ 3i}^2\boldsymbol{e}_2+\Gamma_{\ 3i}^3\boldsymbol{e}_3)\] 成分ごとに並び替え、第\(\mu\)成分は、 \[(\partial_iA^\mu+A^0\Gamma_{\ 0i}^\mu+A^1\Gamma_{\ 1i}^\mu+A^2\Gamma_{\ 2i}^\mu+A^3\Gamma_{\ 3i}^\mu)\boldsymbol{e}_\mu\] \[=\left(\partial_iA^\mu+\sum_{\alpha=0}^3A^\alpha\Gamma_{\ \alpha i}^\mu\right)\boldsymbol{e}_\mu\] 縮約記法を使うと、 \[\nabla_i A^{\mu}=\partial_iA^{\mu}+\Gamma_{\ \alpha i}^{\mu}A^{\alpha}\] ２次元でやった時と同じ結果が得られた。

終わり*/