今回も局所座標。双対な基底ベクトルについて知っている方は飛ばしてもらって大丈夫です。つまずくような難しい話でないので、できるだけ簡単に説明します。

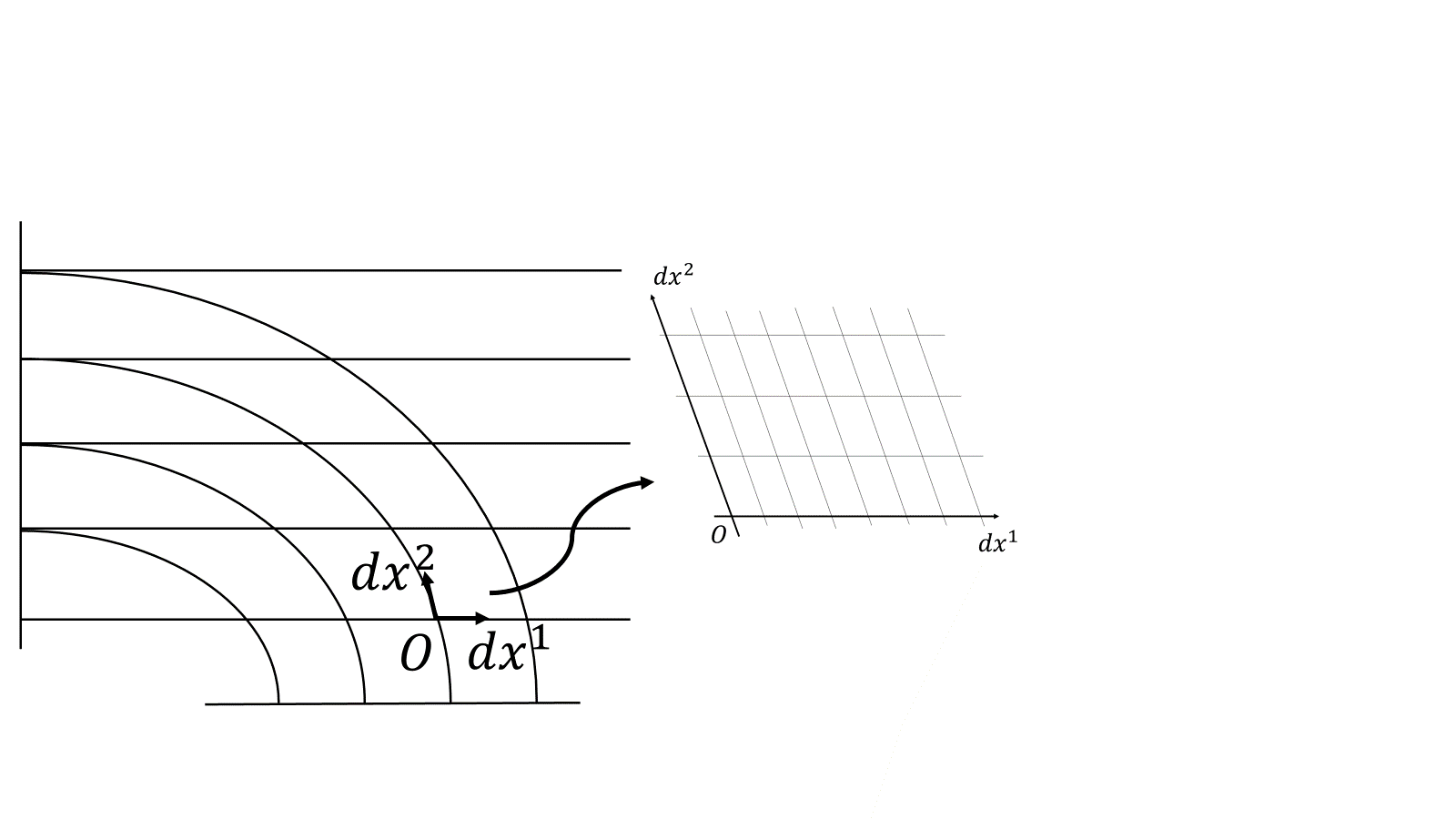
歪んだ空間(軸が曲がっている)の局所座標は、斜めった空間(軸はまっすぐであるが直交しているとは限らない。)とみなせる。

　双対とは一言でいうと\(e_iu^j=\delta_i^{\ j}\)となる\(e_i,u^j\)の関係性であるが、何なのか分かりにくいと思うので、例を出そう。この斜交座標の基底ベクトルを \[\boldsymbol{e}_1=\begin{pmatrix}1\\0\end{pmatrix},\ \boldsymbol{e}_2=\begin{pmatrix}-1/2\\2\end{pmatrix}\] とする。この時直交座標で、\(\boldsymbol{a}=(a_x,a_y)=(2,\ 4)\)で表せるベクトルは、 \[\boldsymbol{a}=a^1\boldsymbol{e}_1+a^2\boldsymbol{e}_2=3\boldsymbol{e}_1+2\boldsymbol{e}_2\] のように表すことができる。直交座標での内積は、 \[\boldsymbol{a}\cdot\boldsymbol{a}=\hat{\boldsymbol{x}}\cdot\hat{\boldsymbol{x}}a_xa_x+\hat{\boldsymbol{x}}\cdot\hat{\boldsymbol{y}}a_xa_y\] \[+\hat{\boldsymbol{y}}\cdot\hat{\boldsymbol{x}}a_ya_x+\hat{\boldsymbol{y}}\cdot\hat{\boldsymbol{y}}a_ya_y\] \(\hat{\boldsymbol{x}}\cdot\hat{\boldsymbol{x}}=\hat{\boldsymbol{y}}\cdot\hat{\boldsymbol{y}}=1,\ \hat{\boldsymbol{x}}\cdot\hat{\boldsymbol{y}}=\hat{\boldsymbol{y}}\cdot\hat{\boldsymbol{x}}=0\)なので、 \[\boldsymbol{a}\cdot\boldsymbol{a}=a_x^2+a_y^2\] \[=2^2+4^2=20\] のように計算できる。斜交座標ではどうだろうか。 \[\boldsymbol{a}\cdot\boldsymbol{a}=\boldsymbol{e}_1\cdot\boldsymbol{e}_1a^1a^1+\boldsymbol{e}_1\cdot\boldsymbol{e}_2a^1a^2\] \[+\boldsymbol{e}_2\cdot\boldsymbol{e}_1a^2a^1+\boldsymbol{e}_2\cdot\boldsymbol{e}_2a^2a^2\] \[\boldsymbol{a}\cdot\boldsymbol{a}=(1+0)a^1a^1+\frac{-1}{2}a^1a^2+\frac{-1}{2}a^2a^1+\left(\frac{1}{4}+4\right)a^2a^2\] \[\boldsymbol{a}\cdot\boldsymbol{a}=(a^1)^2-a^1a^2+\frac{17}{4}(a^2)^2\] となりあまりきれいな形にならない。 \[(a^1)^2-a^1a^2+\frac{17}{4}(a^2)^2\] \[=3^2-3\times2+\frac{17}{4}\times2^2=20\] そこで、\(\boldsymbol{e}_1=(1,0),\ \boldsymbol{e}_2=(-1/2,2)\)の基底ベクトルについて、 \[\boldsymbol{e}_1\cdot\boldsymbol{e}^1=1,\ \boldsymbol{e}_1\cdot\boldsymbol{e}^2=0\] \[\boldsymbol{e}_2\cdot\boldsymbol{e}^1=0,\ \boldsymbol{e}_2\cdot\boldsymbol{e}^2=1\] となるよう、都合よく作られた基底ベクトル\(\boldsymbol{e}^1=(e^1_x,e^1_y),\ \boldsymbol{e}^2=(e^2_x,e^2_y)\)を双対なベクトルという。 \[\begin{cases}\boldsymbol{e}_1\cdot\boldsymbol{e}^1=e^1_x+0=1\\\boldsymbol{e}_2\cdot\boldsymbol{e}^1=-\frac{1}{2}e^1_x+2e^1_y=0\end{cases}\] \[\begin{cases}\boldsymbol{e}_1\cdot\boldsymbol{e}^2=e^2_x+0=0\\\boldsymbol{e}_2\cdot\boldsymbol{e}^2=-\frac{1}{2}e^2_x+2e^2_y=1\end{cases}\] の連立方程式を解くことで、 \[\boldsymbol{e}^1=\begin{pmatrix}1\\1/4\end{pmatrix},\ \boldsymbol{e}^2=\begin{pmatrix}0\\1/2\end{pmatrix}\] と求めることができる。この双対な基底ベクトルを使うことで、\(\boldsymbol{a}=(2,4)\)は、 \[\boldsymbol{a}=a_1\boldsymbol{e}^1+a_2\boldsymbol{e}^2=2\boldsymbol{e}^1+7\boldsymbol{e}^2\]

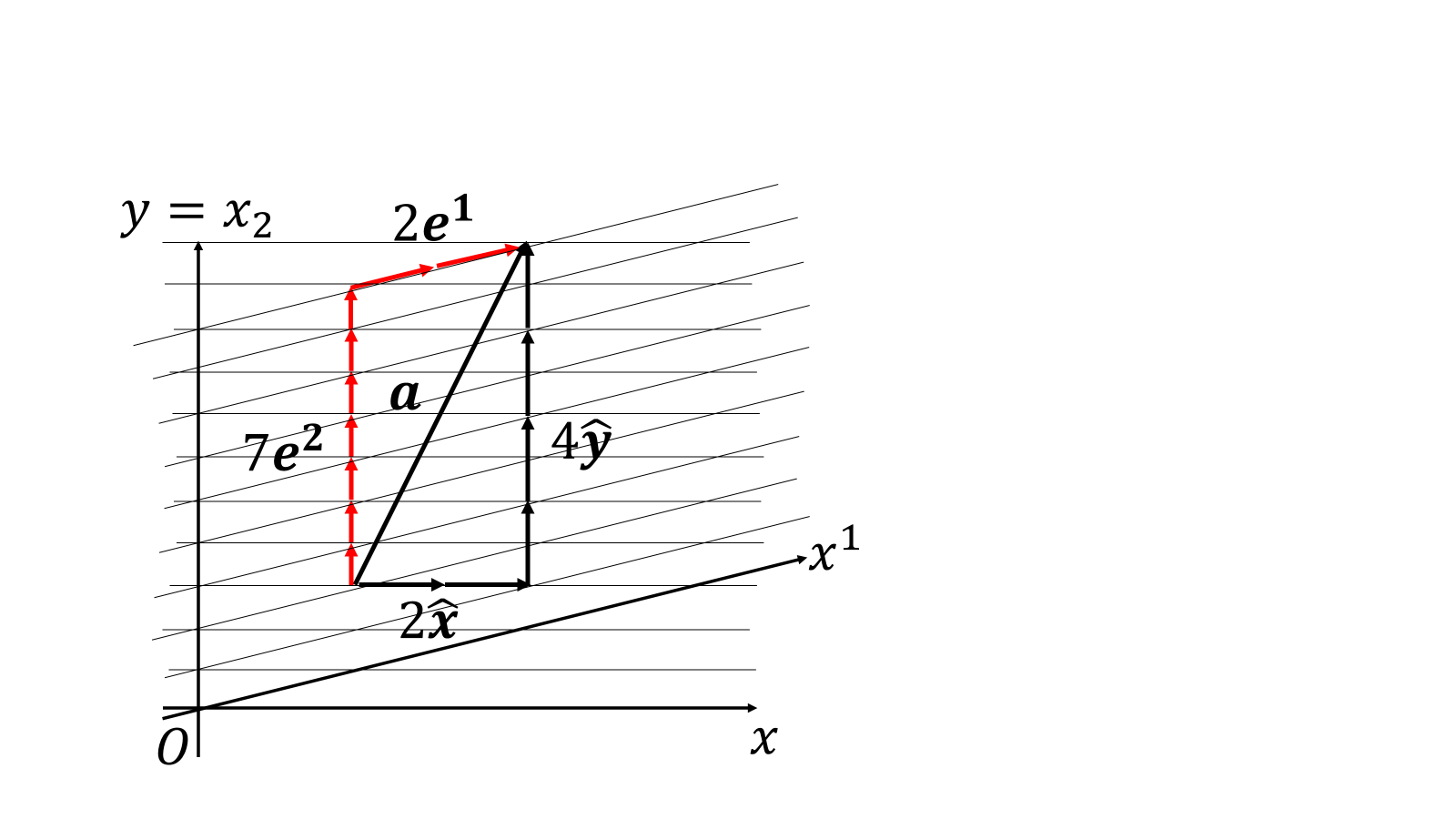
斜交座標では基底ベクトルを使って、 \[\boldsymbol{a}=a^1\boldsymbol{e}_1+a^2\boldsymbol{e}_2\] 双対な基底ベクトルを使って、 \[\boldsymbol{a}=a_1\boldsymbol{e}^1+a_2\boldsymbol{e}^2\] のようにベクトルを２通りの表し方がある。

＊＊双対基底＊＊

　基底ベクトル\(\boldsymbol{e}_1,\boldsymbol{e}_2\)について、 \[\boldsymbol{e}_i\cdot\boldsymbol{e}^j=\begin{cases}1\quad(i=j)\\0\quad(i\neq j)\end{cases}\] となるような基底ベクトル\(\boldsymbol{e}^1,\boldsymbol{e}^2\)となるような基底ベクトルを双対な基底ベクトルという。

　今の段階だと、双対なベクトルを使って、 \[\boldsymbol{a}\cdot\boldsymbol{a}=(a^1\boldsymbol{e}_1+a^2\boldsymbol{e}_2)\cdot(a_1\boldsymbol{e}^1+a_2\boldsymbol{e}^2)\] \[=\boldsymbol{e}_1\cdot\boldsymbol{e}^1a^1a_1+\boldsymbol{e}_1\cdot\boldsymbol{e}^2a^1a_2\] \[+\boldsymbol{e}_2\cdot\boldsymbol{e}^1a^2a_1+\boldsymbol{e}_2\cdot\boldsymbol{e}^2a^2a_2\] \[\boldsymbol{a}\cdot\boldsymbol{a}=a^1a_1+a^2a_2\] 内積をきれいに表現するためのものに見えるかもしれないが、この双対のおかげでクリストッフェルの記号の正体についてまた一歩近づいたのだ。

/*　蛇足

ミンコフスキー空間でのベクトル\(A^{\mu},\ B^\mu\)について、内積は、 \[(A^\mu\boldsymbol{e}_\mu)\cdot(B^\nu\boldsymbol{e}_\nu)\] \[=(A^0\boldsymbol{e}_0+\cdots+A^3\boldsymbol{e}_3)\cdot(B^0\boldsymbol{e}_0+\cdots+B^3\boldsymbol{e}_3)\] \[=\boldsymbol{e}_0\cdot\boldsymbol{e}_0A^0B^0+\cdots+\boldsymbol{e}_0\cdot\boldsymbol{e}_3A^0B^3\] \[+\boldsymbol{e}_1\cdot\boldsymbol{e}_0A^1B^0+\cdots+\boldsymbol{e}_1\cdot\boldsymbol{e}_3A^1B^3\] \[\cdots\] \[+\boldsymbol{e}_3\cdot\boldsymbol{e}_0A^1B^0+\cdots+\boldsymbol{e}_3\cdot\boldsymbol{e}_3A^3B^3\] \[=-A^0B^0+A^1B^1+A^2B^2+A^3B^3\tag{1}\] のように計算できる。 \[\boldsymbol{e}_\mu\cdot\boldsymbol{e}^\nu=\begin{cases}1&(\mu=\nu)\\0&(\mu\neq\nu)\end{cases}\tag{2}\] 双対な基底ベクトル\(\boldsymbol{e}^\mu\)は、(1)(2)を満たさなくてはならないので、 \[\boldsymbol{e}^0=-\boldsymbol{e}_0,\ \boldsymbol{e}^1=\boldsymbol{e}_1,\ \boldsymbol{e}^2=\boldsymbol{e}_2,\ \boldsymbol{e}^3=\boldsymbol{e}_3\] となる。通常の基底を使ってベクトル\(A^{\mu}\)は \[\boldsymbol{A}=A^0\boldsymbol{e}_0+A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2+A^3\boldsymbol{e}_3\] \[=(-A^0)(-\boldsymbol{e}_0)+A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2+A^3\boldsymbol{e}_3\] のように表せる。双対基底を使うと、ベクトル\(\boldsymbol{A}\)は \[\boldsymbol{A}=(-A^0)\boldsymbol{e}^0+A^1\boldsymbol{e}^1+A^2\boldsymbol{e}^2+A^3\boldsymbol{e}^3\] \[=\boldsymbol{A}=A_0\boldsymbol{e}^0+A_1\boldsymbol{e}^1+A_2\boldsymbol{e}^2+A_3\boldsymbol{e}^3\] のようにも表現できる。特殊相対性理論で出てきた\(A_{\mu}\)のような下付き添え字の物理量は双対なベクトルということなのである。双対について触れなかったがその一例を既に使っている。

終わり　/*