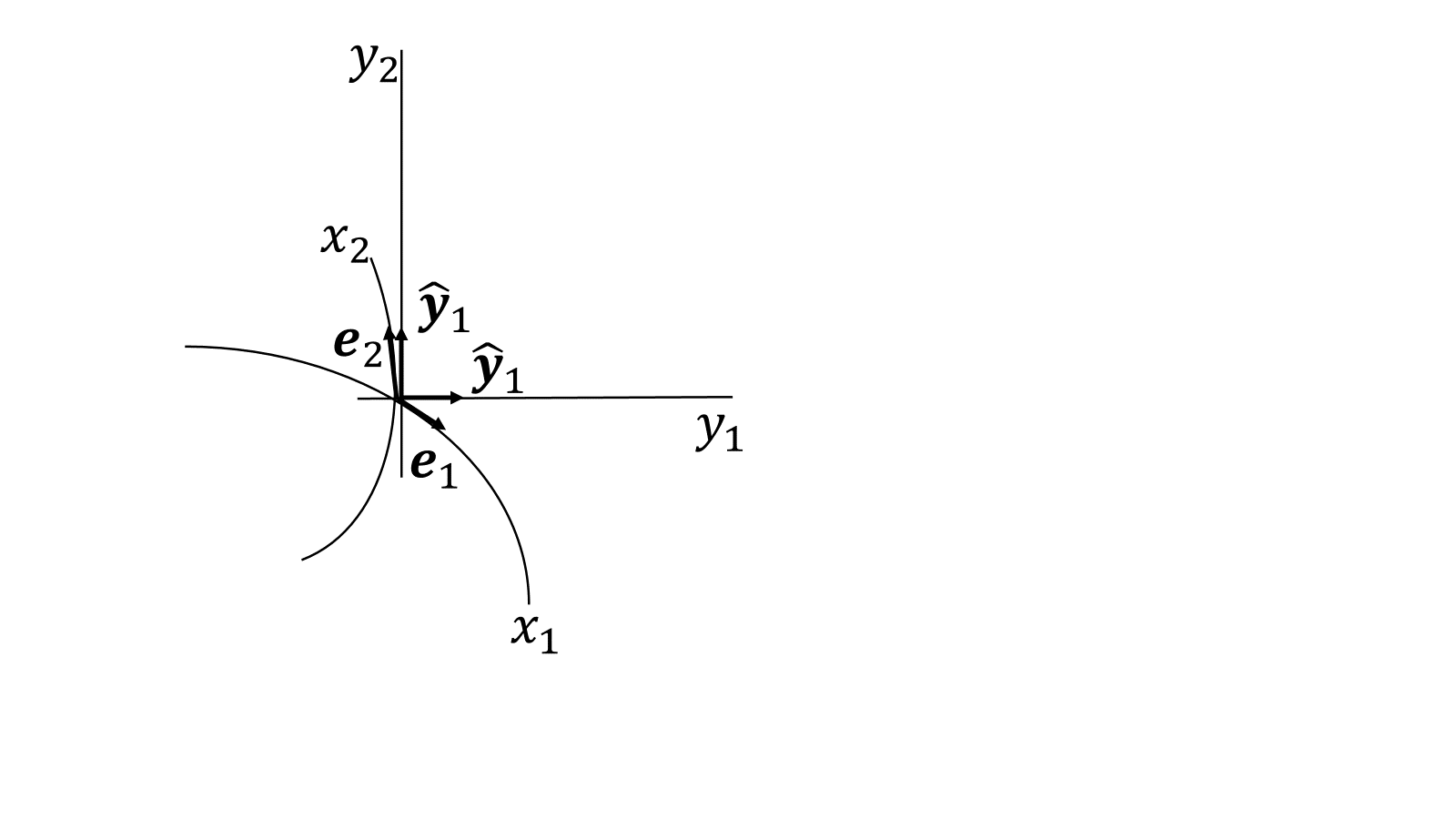クリストッフェルの記号を計量テンソル\(g_{\mu\nu}\)を使って表現するためだけのページ。

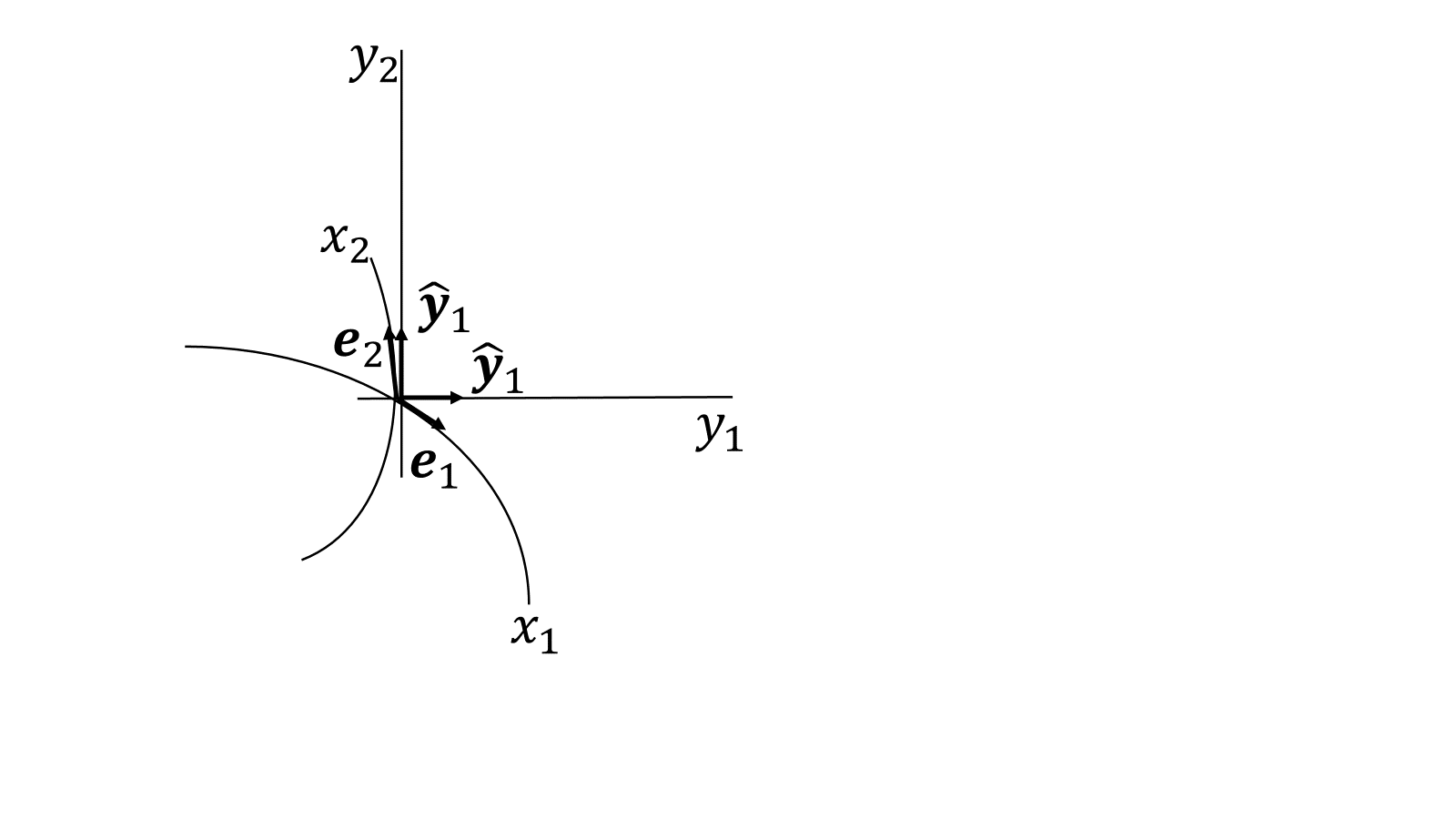
　ここからずっと局所座標の話である。基底ベクトルの表現方法について、\(\boldsymbol{e}_i\)を\(\partial_i\)のように書いてもよいと思っている方は読み飛ばしてもらっていいです。 微小ベクトルが曲がった空間で、 \[d\boldsymbol{x}=dx^1\boldsymbol{e}_1+dx^2\boldsymbol{e}_2\] 直交座標で、 \[d\boldsymbol{x}=dy^1\hat{\boldsymbol{y}}_1+dy^1\hat{\boldsymbol{y}}_2\] のように与えれたとしよう。微小距離の２乗は \[|d\boldsymbol{x}|^2=\boldsymbol{e}_\mu\cdot\boldsymbol{e}_\nu dx^\mu dx^\nu\] 直交座標では \[|d\boldsymbol{x}|^2=(dy^1)^2+(dy^2)^2\] である。２つの座標で、 \[dy^{i}=\frac{\partial y^{i}}{\partial x^1}dx^1+\frac{\partial y^{i}}{\partial x^2}dx^2\] のような座標変換が成り立つはずなので、 \[\boldsymbol{e}_\mu\cdot\boldsymbol{e}_\nu dx^\mu dx^\nu=(dy^1)^2+(dy^2)^2\] \[=\left(\frac{\partial y^{1}}{\partial x^1}dx^1+\frac{\partial y^{1}}{\partial x^2}dx^2\right)^2+\left(\frac{\partial y^{2}}{\partial x^1}dx^1+\frac{\partial y^{2}}{\partial x^2}dx^2\right)^2\] 縮約をしやすいように並べ替える。 \[=\left(\frac{\partial y^{1}}{\partial x^1}\frac{\partial y^{1}}{\partial x^1}+\frac{\partial y^{2}}{\partial x^1}\frac{\partial y^{2}}{\partial x^1}\right)dx^1dx^1\] \[+\left(\frac{\partial y^{1}}{\partial x^1}\frac{\partial y^{1}}{\partial x^2}+\frac{\partial y^{2}}{\partial x^1}\frac{\partial y^{2}}{\partial x^2}\right)dx^1dx^2\] \[+\left(\frac{\partial y^{1}}{\partial x^2}\frac{\partial y^{1}}{\partial x^1}+\frac{\partial y^{2}}{\partial x^2}\frac{\partial y^{2}}{\partial x^1}\right)dx^2dx^1\] \[+\left(\frac{\partial y^{1}}{\partial x^2}\frac{\partial y^{1}}{\partial x^2}+\frac{\partial y^{2}}{\partial x^2}\frac{\partial y^{2}}{\partial x^2}\right)dx^2dx^2\] まずは、一番後ろの\(dx\)について縮約を取ると、 \[=\left(\frac{\partial y^{1}}{\partial x^1}\frac{\partial y^{1}}{\partial x^\nu}+\frac{\partial y^{2}}{\partial x^1}\frac{\partial y^{2}}{\partial x^\nu}\right)dx^1dx^\nu\] \[+\left(\frac{\partial y^{1}}{\partial x^2}\frac{\partial y^{1}}{\partial x^\nu}+\frac{\partial y^{2}}{\partial x^2}\frac{\partial y^{2}}{\partial x^\nu}\right)dx^2dx^\nu\] も一度\(dx\)について縮約を取る。 \[\boldsymbol{e}_\mu\cdot\boldsymbol{e}_\nu dx^\mu dx^\nu=\left(\frac{\partial y^{1}}{\partial x^\mu}\frac{\partial y^{1}}{\partial x^\nu}+\frac{\partial y^{2}}{\partial x^\mu}\frac{\partial y^{2}}{\partial x^\nu}\right)dx^\mu dx^\nu\] つまり、 \[\boldsymbol{e}_\mu\cdot\boldsymbol{e}_\nu=\frac{\partial y^{1}}{\partial x^\mu}\frac{\partial y^{1}}{\partial x^\nu}+\frac{\partial y^{2}}{\partial x^\mu}\frac{\partial y^{2}}{\partial x^\nu}\] これが得たかった式である。基底ベクトルの内積がこのように表せるため、基底ベクトルは \[\boldsymbol{e}_\mu=\begin{pmatrix}\partial y^{1}/\partial x^\mu\\\partial y^{2}/\partial x^\mu\end{pmatrix}=\frac{\partial}{\partial x^{\mu}}\begin{pmatrix}y^{1}\\y^{2}\end{pmatrix}\] こうなると思われる。

/*　補足

　基底ベクトルがそれがもつ成分の偏微分で表せることが重要で、何か別の座標から変換されたという情報\(y^1,y^2\)は、どうでもいいので、 \[\boldsymbol{e}_\mu:=\frac{\partial}{\partial x^{\mu}}=\partial_\mu\] のようにしている教本がほとんどだ。偏微分の演算子だけで基底ベクトルを表すことを不自然に感じるのであれば、\(\partial y^\mu/\partial x^\nu\)のように書けばいいと思う。仮に\(y^1,y^2\)が直交座標だとしたら、\(\partial y^\mu/\partial x^\nu\)は曲がった軸方向の傾きを示すので図形的意味もくみ取れる。

終わり*/

＊＊歪んだ空間の基底ベクトル＊＊

　直交座標\(ℝ^2(y^1,y^2)\)、歪んだ平面\(K(x^1,x^2)\)があり、ある点\(P\)の座標が、\((y^1,y^2),\ (x^1,x^2)\)で表せるとき\(K\)の基底ベクトルは、 \[\boldsymbol{e}_\mu:=\begin{pmatrix}\partial y^{1}/\partial x^\mu\\\partial y^{2}/\partial x^\mu\end{pmatrix}=\frac{\partial}{\partial x^{\mu}}\begin{pmatrix}y^{1}\\y^{2}\end{pmatrix}\]

　どのように表記するにしろ基底ベクトルが同じ成分の偏微分で表せる。クリストッフェルの記号を偏微分を使って表記すると、 \[\Gamma^{\xi}_{\ \mu\nu}\boldsymbol{e}_\xi=\frac{\partial\boldsymbol{e}_\mu}{\partial x^\nu}\] \[\Gamma^{\xi}_{\ \mu\nu}\frac{\partial}{\partial x^\xi}\begin{pmatrix}y^{1}\\y^{2}\end{pmatrix}=\frac{\partial}{\partial x^\nu}\frac{\partial}{\partial x^\mu}\begin{pmatrix}y^{1}\\y^{2}\end{pmatrix}\] 偏微分の順番を変えると、 \[\frac{\partial}{\partial x^\mu}\frac{\partial}{\partial x^\nu}\begin{pmatrix}y^{1}\\y^{2}\end{pmatrix}=\frac{\partial}{\partial x^\nu}\frac{\partial}{\partial x^\mu}\begin{pmatrix}y^{1}\\y^{2}\end{pmatrix}=\Gamma^{\xi}_{\ \nu\mu}\frac{\partial}{\partial x^\xi}\begin{pmatrix}y^{1}\\y^{2}\end{pmatrix}\] クリストッフェルの記号は\(\Gamma^{\xi}_{\ \mu\nu}=\Gamma^{\xi}_{\ \nu\mu}\)下付きの添え字は交換してよいことが分かる。基底ベクトルの偏微分も、 \[\frac{\partial\boldsymbol{e}_\mu}{\partial x^\nu}=\frac{\partial}{\partial x^\nu}\frac{\partial}{\partial x^\mu}\begin{pmatrix}y^{1}\\y^{2}\end{pmatrix}=\frac{\partial}{\partial x^\mu}\frac{\partial}{\partial x^\nu}\begin{pmatrix}y^{1}\\y^{2}\end{pmatrix}=\frac{\partial\boldsymbol{e}_\nu}{\partial x^\mu}\] のように添え字を交換できる。 基底ベクトル\(\boldsymbol{e}_\mu\)の\(\nu\)方向の微分は、 \[\partial_\nu\boldsymbol{e}_\mu=\Gamma^{1}_{\ \mu\nu}\boldsymbol{e}_1+\Gamma^{2}_{\ \mu\nu}\boldsymbol{e}_2\] である。両辺に\(\boldsymbol{e}_{1}\)または\(\boldsymbol{e}_{2}\)の内積を取る。 \[\begin{cases}\boldsymbol{e}_{1}\cdot\partial_\nu\boldsymbol{e}_\mu=g_{11}\Gamma^{1}_{\ \mu\nu}+g_{12}\Gamma^{2}_{\ \mu\nu} \\\boldsymbol{e}_{2}\cdot\partial_\nu\boldsymbol{e}_\mu=g_{21}\Gamma^{1}_{\ \mu\nu}+g_{12}\Gamma^{2}_{\ \mu\nu}\end{cases}\] これを行列を使って表すと、 \[\begin{pmatrix}\boldsymbol{e}_{1}\cdot\partial_\nu\boldsymbol{e}_\mu\\\boldsymbol{e}_{2}\cdot\partial_\nu\boldsymbol{e}_\mu\end{pmatrix}=\begin{pmatrix}g_{11}&g_{12}\\g_{21}&g_{22}\end{pmatrix}\begin{pmatrix}\Gamma_{\ \mu\nu}^1\\\Gamma_{\ \mu\nu}^2\end{pmatrix}\] 逆行列の性質を使い、 \[\begin{pmatrix}\Gamma_{\mu\nu}^1\\\Gamma_{\mu\nu}^2\end{pmatrix}=\begin{pmatrix}g^{11}&g^{12}\\g^{21}&g^{22}\end{pmatrix}\begin{pmatrix}\boldsymbol{e}_{1}\cdot\partial_\nu\boldsymbol{e}_\mu\\\boldsymbol{e}_{2}\cdot\partial_\nu\boldsymbol{e}_\mu\end{pmatrix}\] この式の\(\xi\)成分は、 \[\Gamma_{\ \mu\nu}^\xi=g^{\xi1}\boldsymbol{e}_{1}\cdot\partial_\nu\boldsymbol{e}_\mu+g^{\xi2}\boldsymbol{e}_{2}\cdot\partial_\nu\boldsymbol{e}_\mu\] 縮約を取ると、 \[\Gamma_{\ \mu\nu}^\xi=g^{\xi\rho}\boldsymbol{e}_{\rho}\cdot\partial_\nu\boldsymbol{e}_\mu\tag{1}\] クリストッフェルの記号\(\Gamma_{\ \mu\nu}^\xi\)は下の添え字を入れ替えてもよいので、\(\Gamma_{\ \mu\nu}^\xi=\Gamma_{\ \nu\mu}^\xi\) \[\Gamma_{\ \mu\nu}^\xi=\Gamma_{\ \nu\mu}^\xi=g^{\xi\rho}\boldsymbol{e}_{\rho}\cdot\partial_\mu\boldsymbol{e}_\nu\tag{2}\] (1)式+(2)式で \[2\Gamma_{\ \mu\nu}^\xi=g^{\xi\rho}(\boldsymbol{e}_{\rho}\cdot\partial_\nu\boldsymbol{e}_\mu+\boldsymbol{e}_{\rho}\cdot\partial_\mu\boldsymbol{e}_\nu)\] 積の微分\(\partial (\boldsymbol{e}_{i}\cdot\boldsymbol{e}_{j})=\boldsymbol{e}_{i}\cdot\partial\boldsymbol{e}_{j}+\boldsymbol{e}_{j}\cdot\partial\boldsymbol{e}_{i}\)をうまく使うと、 \[2\Gamma_{\ \mu\nu}^\xi=g^{\xi\rho}\{\partial_\nu(\boldsymbol{e}_{\rho}\cdot\boldsymbol{e}_\mu)+\partial_\mu(\boldsymbol{e}_{\rho}\cdot\boldsymbol{e}_\nu)-\boldsymbol{e}_\mu\cdot\underline{\partial_\nu\boldsymbol{e}_\rho}-\boldsymbol{e}_\nu\cdot\underline{\partial_\mu\boldsymbol{e}_\rho}\}\] 下線部の偏微分と基底ベクトルの添え字を交換すると、 \[=g^{\xi\rho}\{\partial_\nu(\boldsymbol{e}_{\rho}\cdot\boldsymbol{e}_\mu)+\partial_\mu(\boldsymbol{e}_{\rho}\cdot\boldsymbol{e}_\nu)-\boldsymbol{e}_\mu\cdot\partial_\rho\boldsymbol{e}_\nu-\boldsymbol{e}_\nu\cdot\partial_\rho\boldsymbol{e}_\mu\}\] \[=g^{\xi\rho}\{\partial_\nu(\boldsymbol{e}_{\rho}\cdot\boldsymbol{e}_\mu)+\partial_\mu(\boldsymbol{e}_{\rho}\cdot\boldsymbol{e}_\nu)-\partial_\rho(\boldsymbol{e}_\nu\cdot\boldsymbol{e}_\mu)\}\] 計量テンソルを使うことで、 \[2\Gamma_{\ \mu\nu}^\xi=g^{\xi\rho}(\partial_\nu g_{\rho\mu}+\partial_\mu g_{\rho\nu}-\partial_\rho g_{\mu\nu})\]

＊＊クリストッフェルの記号の正体＊＊

　計量テンソル\(g_{\mu\nu}\)を用いて、クリストッフェルの記号は \[\Gamma_{\ \mu\nu}^\xi=\frac{1}{2}g^{\xi \rho}(\partial_\mu g_{\rho\nu}+\partial_\nu g_{\rho\mu}-\partial_\rho g_{\mu\nu})\] と表せる。

/*　蛇足

　クリストッフェルの記号は上記の定義で、\(\rho\)に関して0から3まで和を取ることで、４次元でも使えるが一応示しておこう。\(\nu\)方向の基底ベクトルの\(\mu\)方向の偏微分は、クリストッフェルの記号を使うことで、 \[\partial_\mu\boldsymbol{e}_\nu=\Gamma_{\ \mu\nu}^0\boldsymbol{e}_0+\cdots+\Gamma_{\ \mu\nu}^3\boldsymbol{e}_3\] のように表せる。この式に\(\boldsymbol{e}_1,\cdots,\boldsymbol{e}_3\)の４つの内積を取った式を並べると、 \[\begin{cases}\boldsymbol{e}_0\cdot\partial_\mu\boldsymbol{e}_\nu=g_{00}\Gamma_{\ \mu\nu}^0+\cdots+g_{03}\Gamma_{\ \mu\nu}^3\\\boldsymbol{e}_1\cdot\partial_\mu\boldsymbol{e}_\nu=g_{10}\Gamma_{\ \mu\nu}^0+\cdots+g_{13}\Gamma_{\ \mu\nu}^3\\\cdots\\\boldsymbol{e}_3\cdot\partial_\mu\boldsymbol{e}_\nu=g_{30}\Gamma_{\ \mu\nu}^0+\cdots+g_{33}\Gamma_{\ \mu\nu}^3\end{cases}\] これを行列を使って表現すると、 \[\begin{pmatrix}\boldsymbol{e}_0\cdot\partial_\mu\boldsymbol{e}_\nu\\\boldsymbol{e}_1\cdot\partial_\mu\boldsymbol{e}_\nu\\\boldsymbol{e}_2\cdot\partial_\mu\boldsymbol{e}_\nu\\\boldsymbol{e}_3\cdot\partial_\mu\boldsymbol{e}_\nu\end{pmatrix}=\begin{pmatrix}g_{00}&g_{01}&g_{02}&g_{03}\\g_{10}&g_{11}&g_{12}&g_{13}\\g_{20}&g_{21}&g_{22}&g_{23}\\g_{30}&g_{31}&g_{32}&g_{33}\end{pmatrix}\begin{pmatrix}\Gamma_{\ \mu\nu}^0\\\Gamma_{\ \mu\nu}^1\\\Gamma_{\ \mu\nu}^2\\\Gamma_{\ \mu\nu}^3\end{pmatrix}\] 一般に\(4\times4\)の逆行列(連立方程式を解く)を得るには膨大な計算が必要であるが、上手いこと逆行列を計算したことにして、 \[\begin{pmatrix}g^{00}&g^{01}&g^{02}&g^{03}\\g^{10}&g^{11}&g^{12}&g^{13}\\g^{20}&g^{21}&g^{22}&g^{23}\\g^{30}&g^{31}&g^{32}&g^{33}\end{pmatrix}\begin{pmatrix}\boldsymbol{e}_0\cdot\partial_\mu\boldsymbol{e}_\nu\\\boldsymbol{e}_1\cdot\partial_\mu\boldsymbol{e}_\nu\\\boldsymbol{e}_2\cdot\partial_\mu\boldsymbol{e}_\nu\\\boldsymbol{e}_3\cdot\partial_\mu\boldsymbol{e}_\nu\end{pmatrix}=\begin{pmatrix}\Gamma_{\ \mu\nu}^0\\\Gamma_{\ \mu\nu}^1\\\Gamma_{\ \mu\nu}^2\\\Gamma_{\ \mu\nu}^3\end{pmatrix}\] の連立方程式の形にすると、 \[\begin{cases}\Gamma_{\ \mu\nu}^0=g^{00}\boldsymbol{e}_0\cdot\partial_\mu\boldsymbol{e}_\nu+\cdots+g^{03}\boldsymbol{e}_3\cdot\partial_\mu\boldsymbol{e}_\nu\\\Gamma_{\ \mu\nu}^1=g^{10}\boldsymbol{e}_0\cdot\partial_\mu\boldsymbol{e}_\nu+\cdots+g^{13}\boldsymbol{e}_3\cdot\partial_\mu\boldsymbol{e}_\nu\\\cdots\\\Gamma_{\ \mu\nu}^0=g^{30}\boldsymbol{e}_0\cdot\partial_\mu\boldsymbol{e}_\nu+\cdots+g^{33}\boldsymbol{e}_3\cdot\partial_\mu\boldsymbol{e}_\nu\end{cases}\] この連立方程式の\(\xi\)番目は、 \[\Gamma_{\ \mu\nu}^\xi=g^{\xi0}\boldsymbol{e}_0\cdot\partial_\mu\boldsymbol{e}_\nu+\cdots+g^{\xi3}\boldsymbol{e}_3\cdot\partial_\mu\boldsymbol{e}_\nu\] \[\Gamma_{\ \mu\nu}^\xi=\sum_{\rho=0}^3g^{\xi\rho}\boldsymbol{e}_\rho\cdot\partial_\mu\boldsymbol{e}_\nu\] あとは2次元の時と一緒である。\(\partial_\mu\boldsymbol{e}_\nu=\partial_\nu\boldsymbol{e}_\mu\)なので、 \[\Gamma_{\ \mu\nu}^\xi=\sum_{\rho=0}^3\frac{1}{2}g^{\xi\rho}(\boldsymbol{e}_\rho\cdot\partial_\mu\boldsymbol{e}_\nu+\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu)\] 内積についても積の微分が使えるので、 \[=\sum_{\rho=0}^3\frac{1}{2}g^{\xi\rho}(\partial_\mu(\boldsymbol{e}_\rho\cdot\boldsymbol{e}_\nu)+\partial_\nu(\boldsymbol{e}_\rho\cdot\boldsymbol{e}_\mu)-\boldsymbol{e}_\nu\cdot\partial_\mu\boldsymbol{e}_\rho-\boldsymbol{e}_\mu\cdot\partial_\nu\boldsymbol{e}_\rho)\] 最後の２項に\(\partial_\mu\boldsymbol{e}_\nu=\partial_\nu\boldsymbol{e}_\mu\)をうまく使うと、 \[=\sum_{\rho=0}^3\frac{1}{2}g^{\xi\rho}(\partial_\mu(\boldsymbol{e}_\rho\cdot\boldsymbol{e}_\nu)+\partial_\nu(\boldsymbol{e}_\rho\cdot\boldsymbol{e}_\mu)-\partial_\rho(\boldsymbol{e}_\mu\cdot\boldsymbol{e}_\rho))\] 計量テンソルを使うと、 \[\Gamma_{\ \mu\nu}^\xi=\frac{1}{2}g^{\xi\rho}(\partial_\mu g_{\rho\nu}+\partial_\nu g_{\rho\mu}-\partial_\rho g_{\mu\nu})\] 縮約記法が使われて、シグマが省略されている点に注意だ。

終わり*/