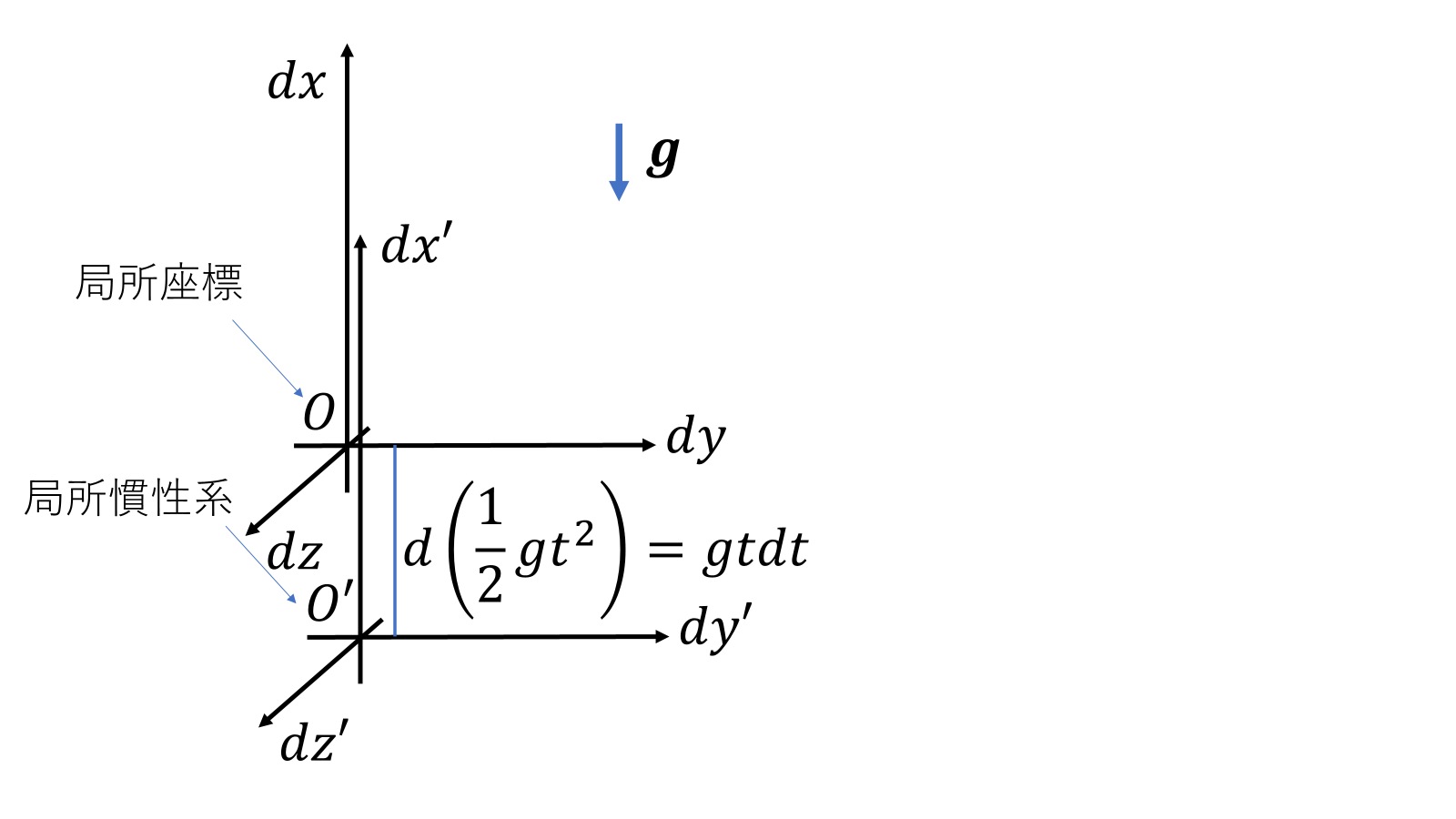特殊相対性理論では、電磁場の基礎方程式であるマクスウェル方程式を矛盾なく説明できた。しかし、重力場でのいくつかの問題をうまく説明できない。一般相対性理論では、強い重力場での時間の遅れや、水星の軌道が楕円でないことが説明できる。

　一般相対性理論での仮定は2つあると思う。

＊＊等価原理＊＊

　重力加速度と同じ加速度で運動している系を局所的に慣性系とみなせる。

＊＊アインシュタイン方程式＊＊

　時空の歪みを表すアインシュタインテンソル\(G_{\mu\nu}\)、運動量エネルギーテンソル\(T_{\mu\nu}\)に比例する。 \[G_{\mu\nu}+\varLambda g_{\mu\nu}=\kappa T_{\mu\nu}\]

　\(\kappa\)は比例係数で大抵の場合\(4\pi G/c^4\)なので、 \[G_{\mu\nu}+\varLambda g_{\mu\nu}=\frac{4\pi G}{c^4} T_{\mu\nu}\] \(\varLambda\)は宇宙定数という定数である。\(\varLambda g_{\mu\nu}\)は宇宙項と言ってあったりなかったりする。太陽系の話をするときには宇宙項は無視される。アインシュタインテンソル\(G_{\mu\nu}\)と運動量エネルギーテンソル\(T_{\mu\nu}\)が比例関係にあるという仮定だ。

　点\(Q\)にある物体が図のような重力場を作るとしよう。重力場が一様とみなせるくらい点\(P\)のごく近くについて、局所座標\(K_P\)を取る。点\(P\)近傍で\(dx'=dx-gtdt\)となるような座標系\(K'_P\)を局所慣性系と呼ぶことにしよう。

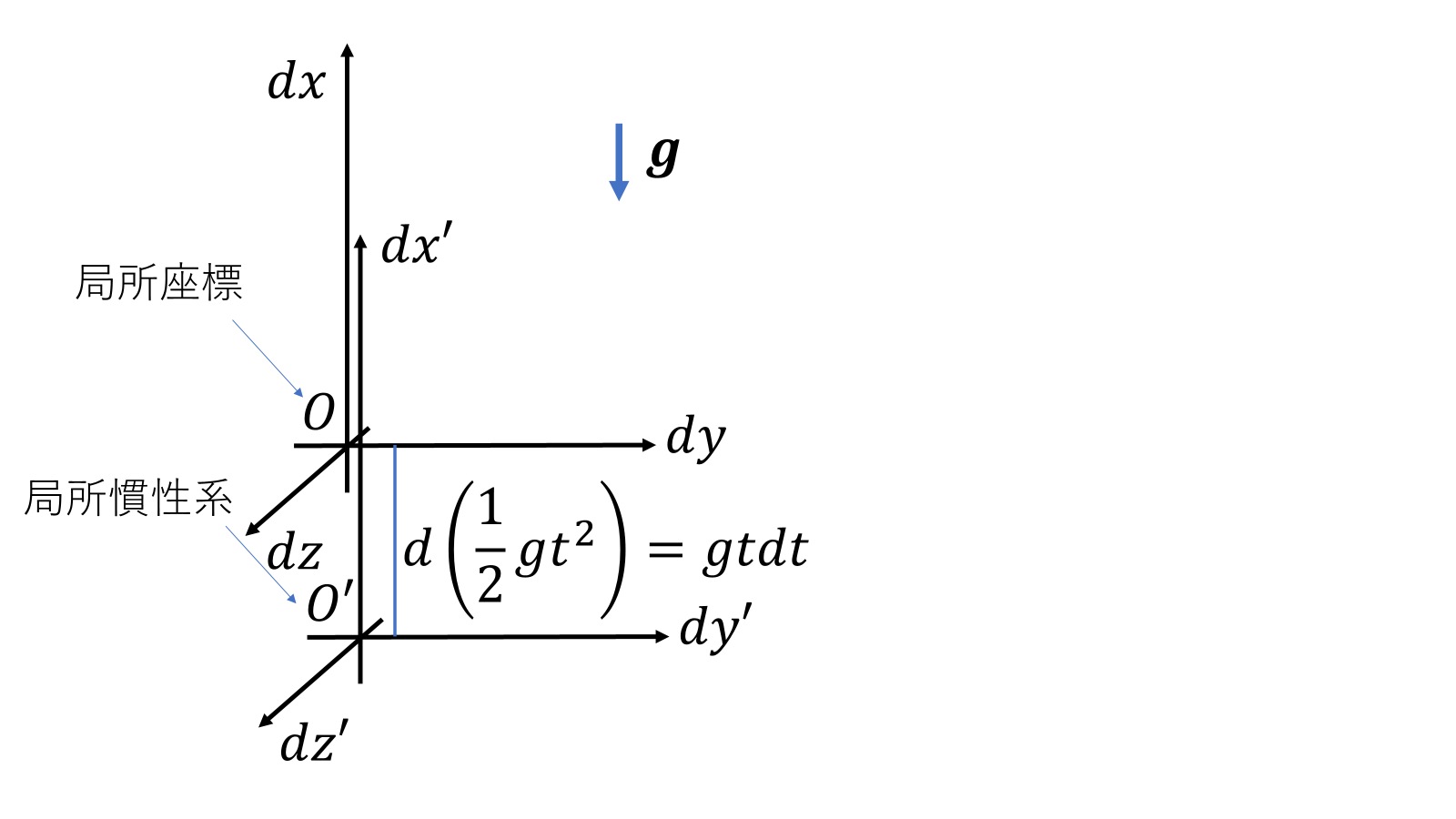
　拡大して書いたが、局所座標\(K_P\)、局所慣性系\(K'_P\)は点とみなせるくらい小さいと思ってほしい。局所慣性系\(K'_P\)の日本語訳が悪い気がするが、慣性系ではない。局所的に\(V=-gt\)の速度で動く"加速度系"である。重力加速度と同じように落下する系なのである。下の階に降りる瞬間のエレベーターや、降下する瞬間の飛行機など重力を感じなくなる瞬間がないだろうか。重力が働いているが、エレベーターが自由落下すれば、重力を全く感じなくなるはず、これがが局所慣性系である。局所慣性系(慣性系とみなしているので)では特殊相対性理論が使える。というよりは、特殊相対性理論が成り立つように計量テンソル\(g_{\mu\nu}\)を変化させるという仮定だと考えるのが一番わかりやすいと思う。要は重力場でも特殊招待性理論が使えるが、計量テンソルが \[g_{\mu\nu}=\begin{cases}-1&(\mu=\nu=0)\\1&(\mu=\nu=1,2,3)\\0&(それ以外)\end{cases}\] ではなくなるということである。具体的な計量テンソルはアインシュタイン方程式を解くことで得ることができる。