関数\(y=f(x)\)は\(x\)に対応する\(y\)が１つ定まるのもである。途中で切れていない関数を連続関数という。図の連続関数\(y=y_1(x)\)の点\(A,\ B\)のような点では接線(関数上のある１点だけで接している直線)を複数取ることができる。連続関数\(y=y_2(x)\)の点\(C\)は接線1つだけ持つ。このとき点\(C\)で微分可能という。ただし図の\(y_2\)は点\(A\)端があるのでこの両端では微分可能ではない。

＊＊曲線の定義＊＊

関数\(y=f(x)\)の任意の\(x\)について、\(x\)付近で接線が１つだけある。つまり傾き\(\frac{dy}{dx}\)が１つに定まる。 \[\frac{dy}{dx}=\lim_{\varDelta x\to0}\frac{f(x+\varDelta x)-f(x)}{\varDelta x}\] このような関数を微分可能な関数、曲線という。

２変数関数\(z=f(x,y)\)はある\(x,y\)の組に対応する\(z\)が１つに定まるもの。2変数関数\(f(x,y)\)上のある点\(D(x_D,y_D)\)について、\(y=y_D\)で固定して得られた関数を\(z=g(x)\)、\(x=x_D\)で固定して得られた関数を\(z=h(y)\)とする。\(g(x)\)の接線を\(z=l_1(x)\)、\(h(y)\)の接線を\(z=l_2(y)\)とする。接線\(l_1,l_2\)が作る平面が接することになる。法線(面に垂直な線)\(y=l_3(x)\)が１つに定まるとも言い換えられる。

＊＊曲面の定義＊＊

関数\(z=f(x,y)\)の任意の\(x,y\)について、\(x,y\)付近で接面が１つだけあるとき、\(\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}\)がそれぞれ１つに定まる。 \[\frac{\partial z}{\partial x}=\lim_{\varDelta x\to0}\frac{f(x+\varDelta x,y)-f(x,y)}{\varDelta x}\] \[\frac{\partial z}{\partial y}=\lim_{\varDelta y\to0}\frac{f(x,y+\varDelta y)-f(x,y)}{\varDelta x}\] このような全関数を微分可能な関数、曲面という。

以後微分を使っていきたいので\(n\)個の変数を持つ関数\(f(x^1,x^2,\cdots,x^i,\cdots,x^n)\)は\(\frac{\partial f}{\partial x^i}\)が１つに定まるものだけ扱うことにしよう。筆者は微分可能か確認しないでいきなり微分するので、その時はそういう関数だと思ってくださいな。更に言うと\(x\)軸上の数字が連続か、数字の大小関係とかあるかも知れないがこれ以上深くはやらないことにしよう。微分の説明終わり。

図の灰色の部分の面積を\(F(a)\)とする。\(a\)は任意の数でいいので、\(F(x)\)は関数になる。を\(F(x)\)を\(f(x)\)の原始関数という。

このような部分の面積\(S(x)\)を\(S(x)=F(x)-F(a)\)と表せる。

\(\varDelta x\)はとても小さい値である。図のような部分の面積\(\varDelta S=F(x+\varDelta x)-F(x)\)を求めるためたい。\(0\le\theta\le1\)を上手く取ることで、(この\(\theta\)がよくわからない方は、微分積分学の基本定理というページで若干詳しく説明している。) \[\varDelta S=f(x+\theta\varDelta x)\varDelta x\tag{1}\] 高さ\(f(x+\theta\varDelta x)\)幅長方形\(\varDelta x\)の面積で表せる。とても大きい数\(n\)で分割して\(a=x_0\le x_1\le\cdots\le x_i\le\cdots\le x_n=x,\ \varDelta x_i=x_{i+1}-x_{i}\)、とすると、 面積\(S(x)\)は \[S(x)=F(x)-F(a)=\sum_{i=0}^{n-1}f(x_i+\theta_i\varDelta x_i)\varDelta x_i\tag{2}\] と表せる。(1)式を変形することで、原始関数\(F(x)\)から\(f(x)\)を求めることもできる。 \[f(x+\theta\varDelta x)=\frac{F(x+\varDelta x)-F(x)}{\varDelta x}\tag{3}\] (2)(3)式は\(\theta\)が上手く求められないので上手く表現できていない。そこで\(\varDelta x\)を0に近づけていこう。 \[\lim_{\varDelta x\to0}\] 記号を上記のように書く。 \[\frac{dF(x)}{dx}:=\lim_{\varDelta x\to0}\frac{F(x+\varDelta x)-F(x)}{\varDelta x}\] \[\int_{a}^xf(x)dx:=\lim_{\varDelta x\to0}\sum_{i=0}^{n-1}f(x_i+\theta_i\varDelta x_i)\varDelta x_i\] と書くことにすると、(2)、(3)式はそれぞれ、 \[\frac{dF(x)}{dx}=f(x)\tag{4}\] \[\int_{a}^xf(x)dx=F(x)-F(a)\tag{5}\] と書くことができる。(4)式を関数\(F(x)\)の微分、(5)式を関数\(f(x)\)の積分という。原始関数\(F(x)\)を微分すると関数\(f(x)\)を得ることができる。逆に関数\(f(x)\)を積分すると、原始関数\(F(x)\)とおまけで\(-F(a)\)が付く。全く真逆の関係では無いようだ。(5)式の\(a\)の値が特に決まっていない場合、 \[\int f(x)dx=F(x)+C\tag{6}\] のように書かれる。\(f(x)=dF(x)/dx\)なので、 \[\int \frac{dF(x)}{dx}dx=F(x)+C\] とも表せられる。

\(x\)が\(t\)を変数とする関数\(x=x(t)\)だった時、\(f(x(t))\)のような合成関数での微分と積分の方法を考える。 \(a=x_0\le x_1\le\cdots\le x_i\le\cdots\le x_n=x,\ \varDelta x_i=x_{i+1}-x_{i}\) のような分割をしていた。\(a=x(t_0)\le x(t_1)\le\cdots\le x(t_i)\le\cdots\le x(t_n)=x\)となるように分割すると、\(x_{i+1}=x(t_i+\varDelta t_i)\)、\(\varDelta x_i=x(t_i+\varDelta t_i)-x(t_i)\)となる。 \[\varDelta S=f(x(t)+\theta\varDelta x)\varDelta x\] \[\varDelta S=f(x(t)+\theta\varDelta x)\frac{x(t+\varDelta t)-x(t)}{\varDelta t}\varDelta t\tag{7}\] (7)式を変形すると \[\frac{F(x(t))-F(x(t+\varDelta t))}{\varDelta t}\] \[=f(x(t)+\theta\varDelta x)\frac{x(t+\varDelta t)-x(t)}{\varDelta t}\tag{8}\] また\(S(x(t))\)の値は、 \[S(x)=F(x)-F(a)=\sum_{i=0}^{n-1}f(x_i+\theta_i\varDelta x_i)\varDelta x_i\] \[=\sum_{i=0}^{n-1}f(x(t_i)+\theta_i\varDelta x_i)\frac{x(t_i+\varDelta t_i)-x(t_i)}{\varDelta t_i}\varDelta t_i\tag{9}\] と書ける。(8)の\(\varDelta t\to0\)、\(\varDelta x\to0\)の極限を取る。 \[\frac{dF(x(t))}{dt}=\lim_{\varDelta t\to0}f(x(t)+\theta\varDelta x)\frac{x(t+\varDelta t)-x(t)}{\varDelta t}=f(x(t))\frac{dx}{dt}\] \[\frac{dF(x(t))}{dt}=f(x(t))\frac{dx}{dt}\tag{10}\] (9)の\(\varDelta t\to0\)、\(\varDelta x\to0\)の極限を取る。 \[F(x(t))-F(a)=\lim_{\varDelta t\to0}\sum_{i=0}^{n-1}f(x(t_i)+\theta_i\varDelta x_i)\frac{x(t_i+\varDelta t_i)-x(t_i)}{\varDelta t_i}\varDelta t_i\] \[F(x(t))-F(a)=\int_{t_0}^{t}f(x(t))\frac{dx}{dt}dt\tag{11}\] \(f(x)=dF(x)/dx\)なので、(10)(11)式はそれぞれ \[\frac{dF(x(t))}{dt}=\frac{dF(x)}{dx}\frac{dx}{dt}\] \[F(x(t))-F(a)=\int_{t_0}^{t}\frac{dF(x)}{dx}\frac{dx}{dt}dt\] のように表すこともできる。

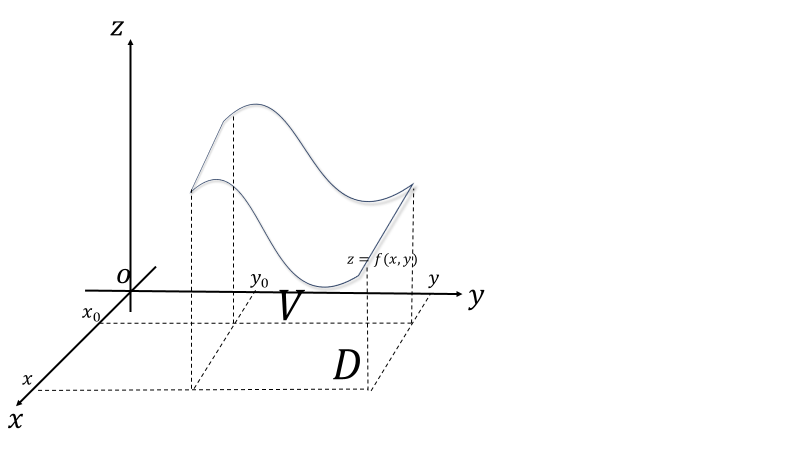
関数\(z=f(x,y)\)について\(f(x,y)\)と辺の長さが\(|x-x_0|\)と\(|y-y_0|\)の領域\(D\)の作る領域の体積を\(V(x,y)\)とする。

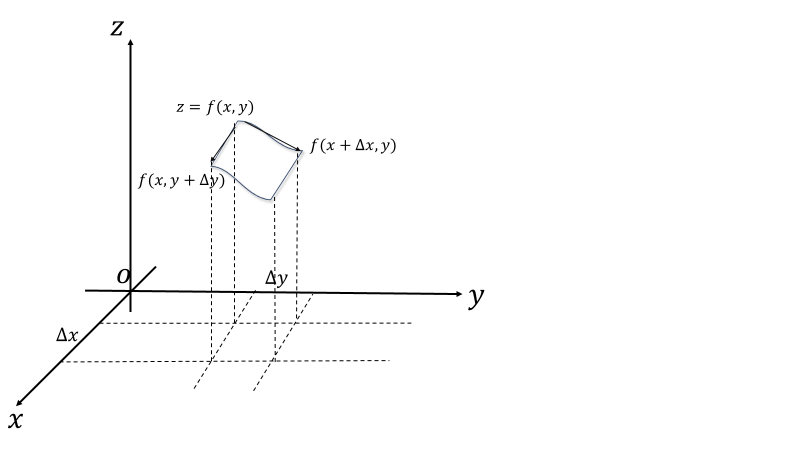
微小量\(\varDelta x,\varDelta y\)と都合のいい数\(0\ge\theta,\iota\ge1\)を使い、図のような部分の体積\(\varDelta V\)を \[\varDelta V=V(x+\varDelta x,y+\varDelta y)-V(x,y)\] \[=f(x+\theta\varDelta x,y+\iota\varDelta y)\varDelta x\varDelta y\tag{12}\] のような直方体の体積で書けるはず。領域\(D\)内で\(x_0\le x_1\le x_2\le\cdots\le x_i\le\cdots\le x_n=x\)の分割をしてする。\(x_i\)を固定して\(z=f(x_i,y)\)を1変数関数とみると、\(x_i\)で固定した、\(y,z\)平面で\(V\)を切り開いた部分の面積は(2)式のように \[S(x_i)=\sum_{j=0}^{m-1}f(x_i,y_j+\iota\varDelta y_j)\varDelta y_j\] とあらわせる。立体の体積\(V\)は \[V(x,y)=\sum_{i=0}^{n-1}S(x_i+\theta\varDelta x_i)\varDelta x_i\] \[V(x,y)=\sum_{i=0}^{n-1}\sum_{j=0}^{m-1}f(x_i+\theta\varDelta x_i,y_j+\iota\varDelta y_j)\varDelta x_i\varDelta y_j\] \(\theta,\iota\)が要らないので、\(\varDelta x,\varDelta y\to 0\)の極限をとると、 \[V(x,y)=\iint_{D}f(x,y)dxdy:=\] \[\lim_{\varDelta x,\varDelta y\to 0}\sum_{i=0}^{n-1}\sum_{j=0}^{m-1}f(x_i+\theta\varDelta x_i,y_j+\iota\varDelta y_j)\varDelta x_i\varDelta y_j\] とあらわせる。

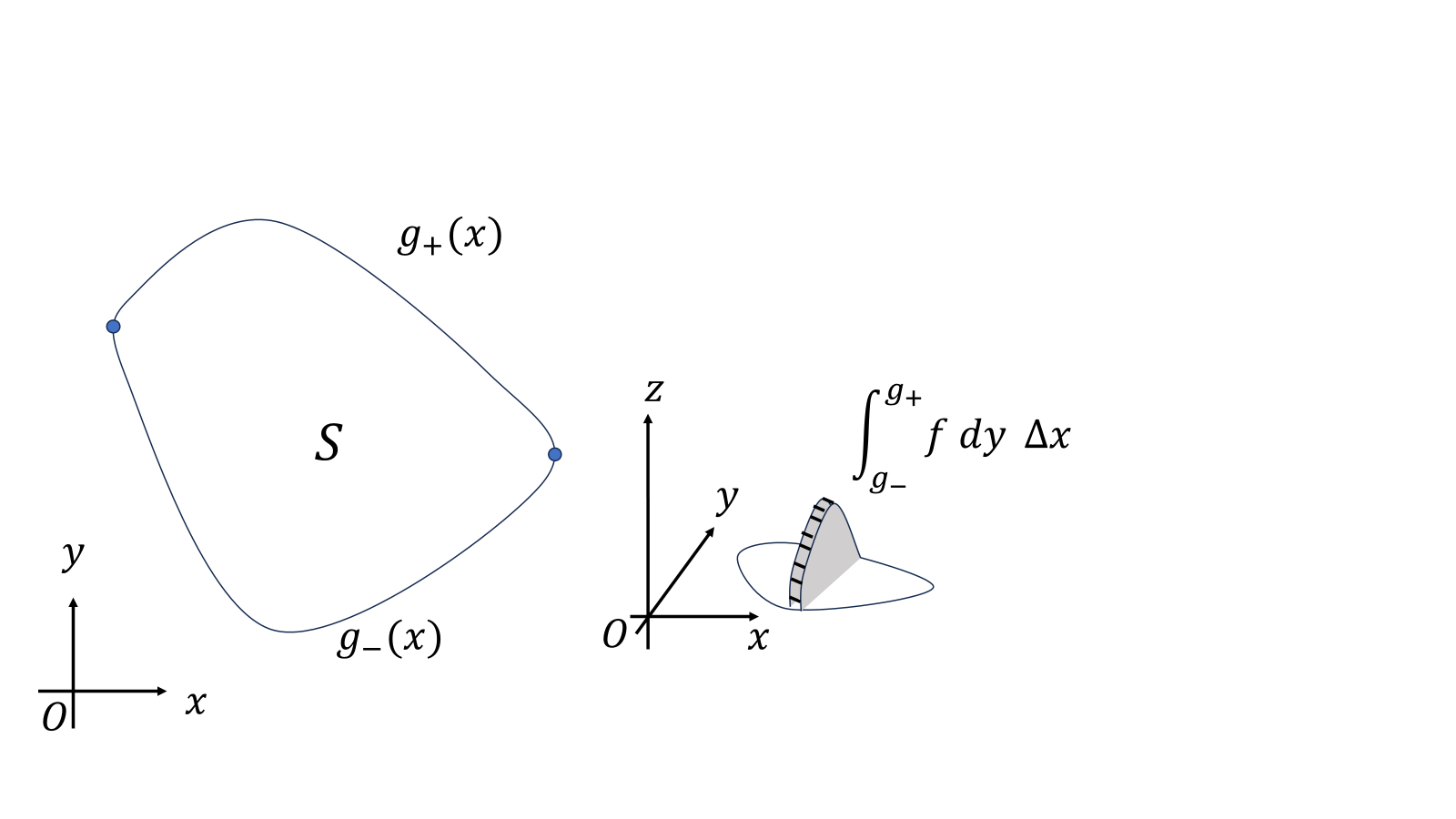
底面が曲線でできている場合にも積分ができる。立体を\(yz\)平面で分割して断面積\(\int_{g_-}^{g_+}f(x,y)dy\)を求めてそれを積分する。 \[V=\iint_Sf(x,y)dxdy=\int_a^b\left(\int_{g_-(x)}^{g_+(x)}f(x,y)dy\right)dx\]

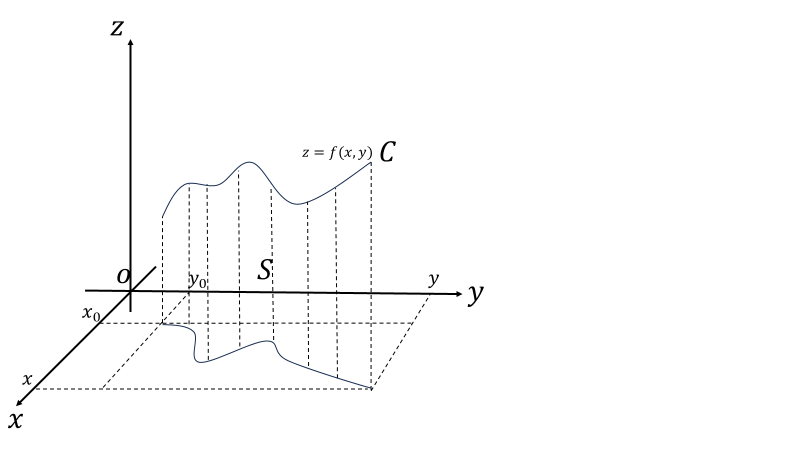
　線積分というものもある。図の面積\(S(x,y)\)を求めたい。図のような曲線\(C\)も２変数関数の１つである。\(y\)に対応した\(x\)が１つ存在するという制限を付けた2変数関数といえる。つまり、\(x\)を決めると\(y\)が決まり、\(x,y\)が決まると経路\(C\)上の１点が決まる。そこで媒介変数\(t\)を使って、\(x=x(t),y=y(t)\)としよう。\(C:z=f(x(t),y(t))\)も\(t\)のみで表せる。\(x(t_0)\le x(t_1)\le\cdots\le x(t_i)\le\cdots\le x(t_n)=x\)、\(y(t_0)\le y(t_1)\le\cdots\le y(t_i)\le\cdots\le y(t_n)=y\)と分割する。\(\Delta x_i=x(t_{i+1})-x(t_{i}),\Delta y_i=y(t_{i+1})-y(t_{i})\)となる。\(\varDelta t_i=t_{i+1}-t_i\)とすれば\(\Delta x_i=x(t_{i}+\varDelta t_{i})-x(t_{i}),\Delta y_i=y(t_{i}+\varDelta t_i)-y(t_{i})\)となるので、

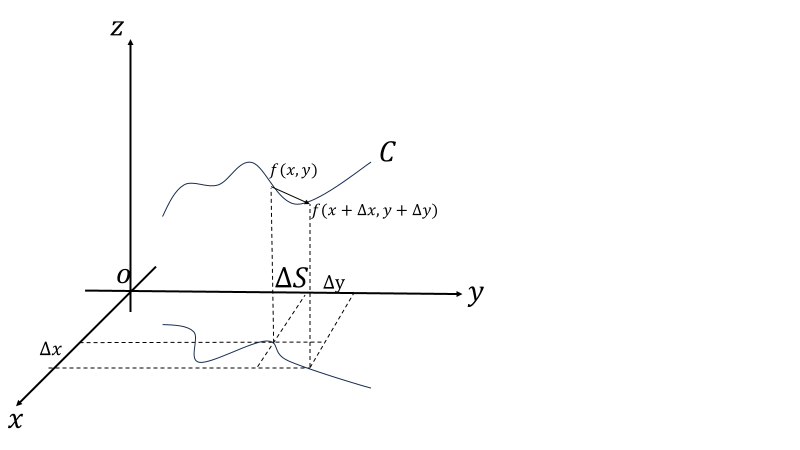
あまり上手いやり方が思いつかなかった、曲面はどう分割しても曲面なものでな。図のような面積\(\varDelta S\)はおおざっぱに \[\varDelta S\simeq f(x,y)\sqrt{\varDelta x^2+\varDelta y^2}\] とあらわせる。\(t\)を使って表すと、 \[\varDelta S\simeq f(x,y)\sqrt{\left(\frac{\varDelta x}{\varDelta t}\right)^2+\left(\frac{\varDelta y}{\varDelta t}\right)^2}\varDelta t\] \[=f(x,y)\sqrt{\left(\frac{x(t+\varDelta t)-x(t)}{\varDelta t}\right)^2+\left(\frac{y(t+\varDelta t)-y(t)}{\varDelta t}\right)^2}\varDelta t\] これを足していくことでおおざっぱな面積を求められる。 \[S\simeq\sum_{i=0}^{n-1} f(x(t_i),y(t_i))\] \[\sqrt{\left(\frac{x(t_i+\varDelta t_i)-x(t_i)}{\varDelta t_i}\right)^2+\left(\frac{y(t_i+\varDelta t_i)-y(t_i)}{\varDelta t_i}\right)^2}\varDelta t_i\] \(\varDelta t\to 0\)の極限で分割を増やしていくことで曲面をより近づいていくと考えてほしい。 \[S=\int_{C}f(x,y)\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\] が成り立つ。