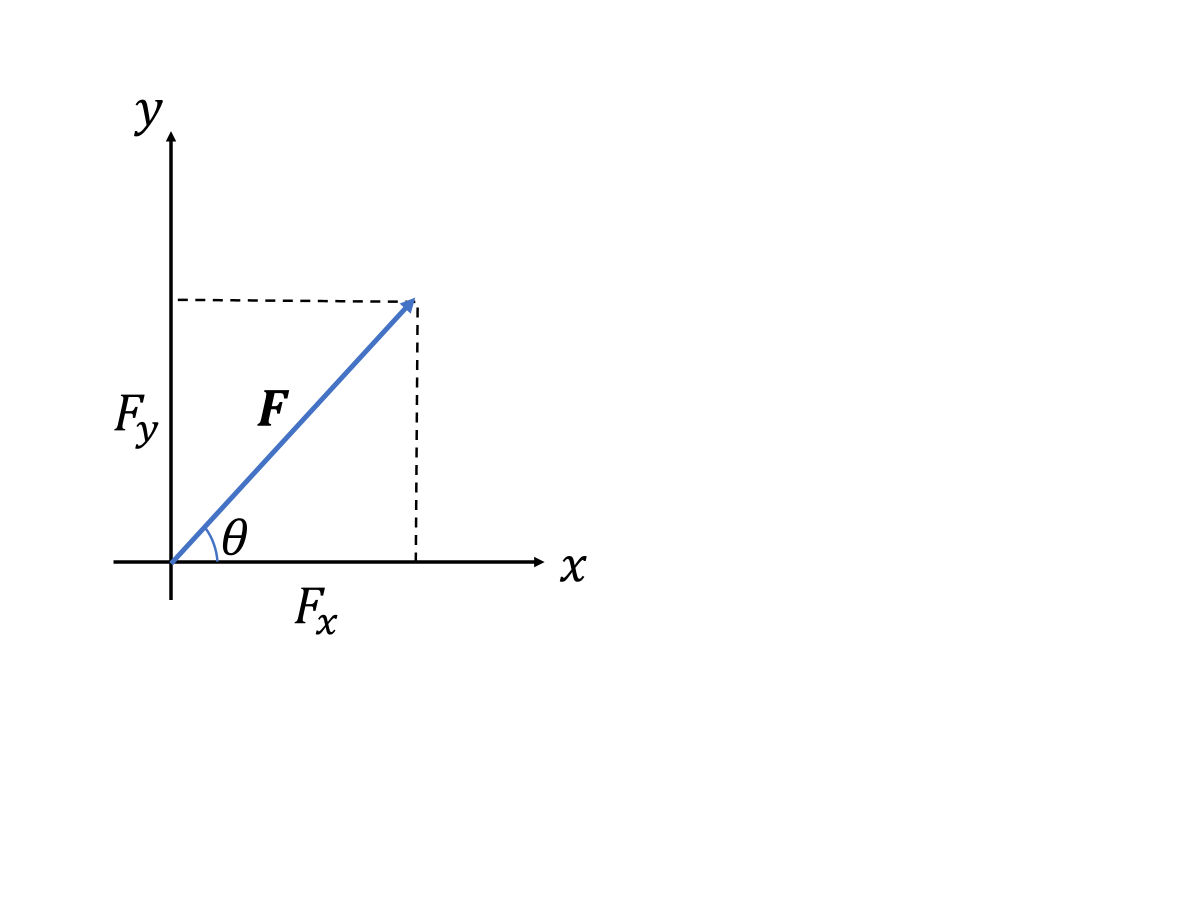楽しい科学（理論）チャンネル

　今回の主役はエネルギーなぜエネルギーは見ることができなく抽象的な概念だがとても便利である。なぜ便利なのかも解説する。ニュートン力学で、力\(\boldsymbol{F}\)は率直で分かりやすい物理量であるが、力は『向き』を持っていることが邪魔になる場合がある。例えば、(熱交換率とかは無視する。)石炭を例にしよう。石炭は蒸気機関車を動かす力を潜在的に持っている。石炭を燃料として使用した場合、石炭が潜在的に持っている力が蒸気機関車が動くことで、力\(\boldsymbol{F}\)として観察できる。しかし、蒸気機関車が逆向きの場合は逆向きに発進するので、石炭による力は\(-\boldsymbol{F}\)となる。

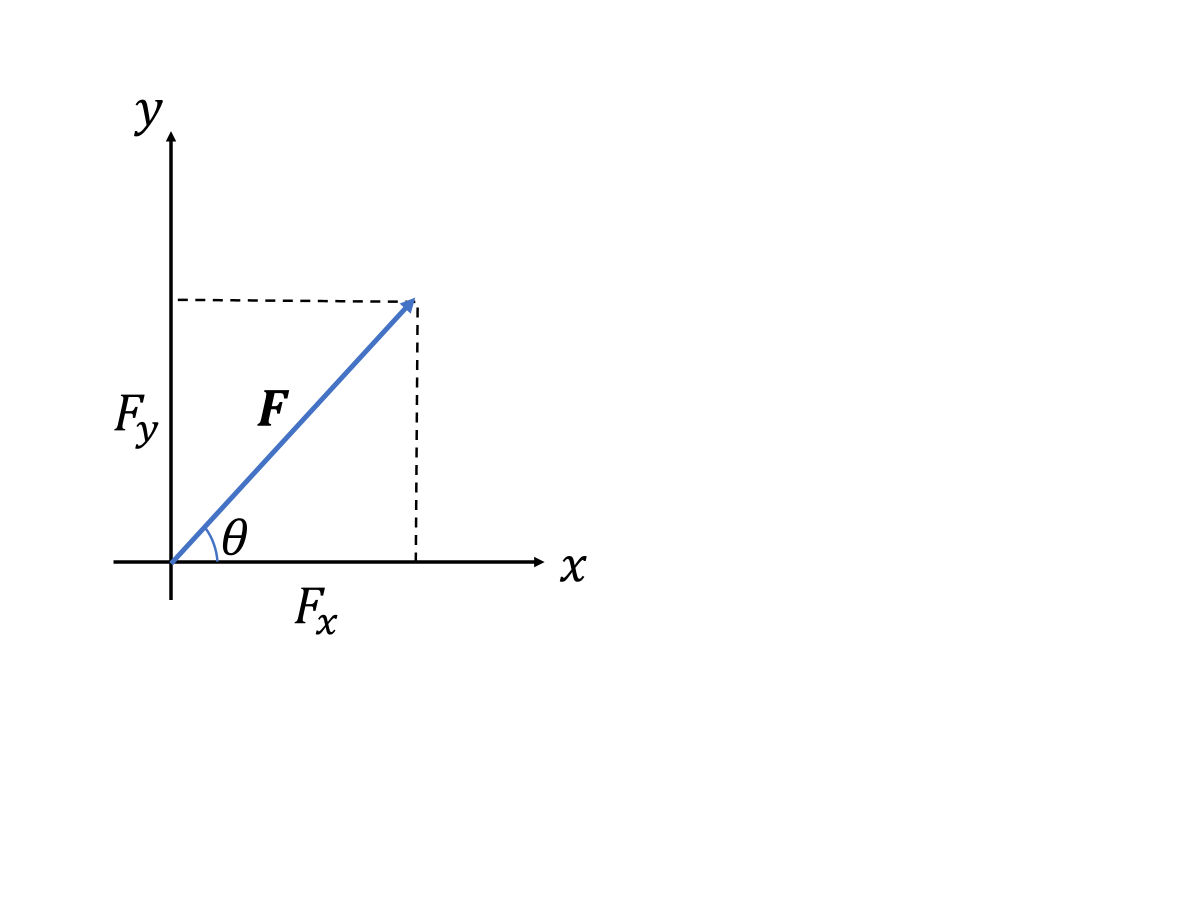
　これを解決する方法として、スカラー(向きのないただの数)力の大きさ\(F\)を使う。 \[F:=|\boldsymbol{F}|=\sqrt{\boldsymbol{F}\cdot\boldsymbol{F}}=\sqrt{F_x^2+F_y^2}\] これにより、石炭が蒸気機関車に入る前の潜在的な力を表すことができた。しかし\(F\)を潜在的な力の指標とするには、良くも悪くも瞬発的な値である。同じ量の石炭が同じ潜在的な力を持っているが、\(F\)は瞬発的な量になっている。石炭を一気に炉に入れるか、ちょっとずつ炉に入れるかで瞬間的に\(F\)が変わってしまう。そこで、移動経路中で力を積分していく仕事という物理量が考えられた。

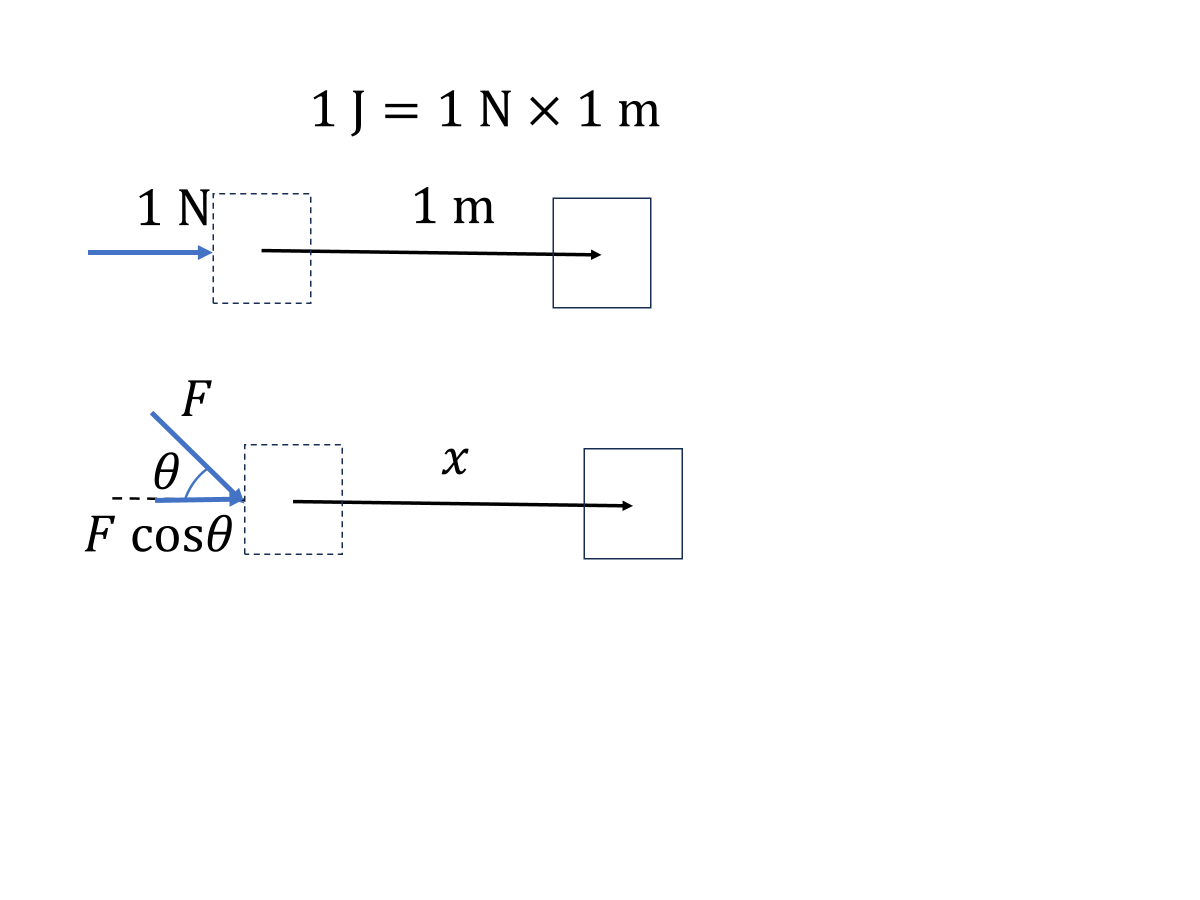
　1Nの力によって力と同じ向きに1m進んだ時、1Jとする。力と移動した経路は同じ向きでなくてはいけいないので、向きが違う場合は、図のように\(W=Fx\cos\theta\)となる。仕事\(W=Fx\cos\theta=\boldsymbol{F}\cdot\boldsymbol{x}\)は、内積を使っているのでスカラーである。経路中で力\(\boldsymbol{F}\)が変化するかもしれないので、積分をする。また直線の経路になっていない可能性もあるので、小さな変位\(d\boldsymbol{x}\)ごとに\(\boldsymbol{F}\)と内積を取り足し合わせていくという意味もある。蒸気機関車も重力を受けているが進行方向と垂直なので、重力の仕事は\(W_{mg}=mgx\cos90^\circ=0\)なっている。

　一般に仕事の値は、経路\(C\)に依存しており経路によって値が変わる。移動している間進行方向と逆に一定の摩擦力や速度に依存した空気抵抗がはたらいている場合の仕事は遠回りの経路のほうが仕事が大きくなる。摩擦や空気抵抗などの力はたらかない場合、物体にはたらく力を\(\boldsymbol{F}(\boldsymbol{x})\)、任意の経路の始点と終点を\(\boldsymbol{x}_0,\ \boldsymbol{x}\)とすると、 \[W_{\boldsymbol{x}_0\to\boldsymbol{x}}=\int_{\boldsymbol{x}_0}^{\boldsymbol{x}}\boldsymbol{F}(\boldsymbol{x})\cdot d\boldsymbol{x}=G(\boldsymbol{x})-G(\boldsymbol{x}_0)\] ポテンシャルエネルギーを次のように定義する。 \[U(\boldsymbol{x}):=U(\boldsymbol{x}_0)-\int_{\boldsymbol{x}_0}^{\boldsymbol{x}}\boldsymbol{F}(\boldsymbol{x})\cdot d\boldsymbol{x}\tag{3}\] 上の式の\(G\)を\(-U\)に置き換えただけである。なぜ符号を変えたかというと \[W_{\boldsymbol{x}_0\to\boldsymbol{x}}=U(\boldsymbol{x}_0)-U(\boldsymbol{x})\] としたかったからである。(3)式からポテンシャルエネルギー\(U(\boldsymbol{x})\)と仕事が経路に依らない力\(\boldsymbol{F}(\boldsymbol{x})\)の関係を見てみよう。 \[U(\boldsymbol{x})-U(\boldsymbol{x}_0)=-\int_{\boldsymbol{x}_0}^{\boldsymbol{x}}\boldsymbol{F}(\boldsymbol{x})\cdot d\boldsymbol{x}\] \[\int_{\boldsymbol{x}_0}^{\boldsymbol{x}}dU(\boldsymbol{x})=-\int_{\boldsymbol{x}_0}^{\boldsymbol{x}}\boldsymbol{F}(\boldsymbol{x})\cdot d\boldsymbol{x}\] \[-dU(\boldsymbol{x})=\boldsymbol{F}(\boldsymbol{x})\cdot d\boldsymbol{x}\tag{4}\] これでも十分にシンプルな関係式だが、もう少し違う形で表してみよう。(4)式の左辺は \[dU(x,y,z)=\frac{\partial U(x,y,z)}{\partial x}dx+\frac{\partial U(x,y,z)}{\partial y}dy+\frac{\partial U(x,y,z)}{\partial z}dz\] である。右辺を成分を使って \[-\frac{\partial U(x,y,z)}{\partial x}dx-\frac{\partial U(x,y,z)}{\partial y}dy-\frac{\partial U(x,y,z)}{\partial z}dz\] \[=F_x(x,y,z)dx+F_y(x,y,z)dy+F_z(x,y,z)dz\] と表せる。長いですな。いかにベクトル表記が式の見通しを良くしているかがわかる。\(dx,dy,dz\)の係数を比較すると、 \[\begin{pmatrix}F_x(x,y,z)\\F_y(x,y,z)\\F_z(x,y,z)\end{pmatrix}=\begin{pmatrix}-\frac{\partial U(x,y,z)}{\partial x}\\-\frac{\partial U(x,y,z)}{\partial y}\\-\frac{\partial U(x,y,z)}{\partial z}\end{pmatrix}\] このようなベクトルの方程式が立つ。 \[\begin{pmatrix}F_x(x,y,z)\\F_y(x,y,z)\\F_z(x,y,z)\end{pmatrix}=-\begin{pmatrix}\frac{\partial}{\partial x}\\\frac{\partial}{\partial y}\\\frac{\partial}{\partial z}\end{pmatrix}U(x,y,z)\] ここで \[\nabla:=\frac{\partial}{\partial x}\boldsymbol{e}_x+\frac{\partial}{\partial y}\boldsymbol{e}_y+\frac{\partial}{\partial z}\boldsymbol{e}_z\] を定義する。これにより、 \[\boldsymbol{F}(\boldsymbol{x})=-\nabla U(\boldsymbol{x})\] が成り立つ。

　注意として\(\nabla U(\boldsymbol{x})\)の積の順番を変えることはできない。\(\nabla\)はスカラー関数をベクトル関数に変える演算であるとともに微分の演算子でもある。\(\frac{d}{dx}f(x)\neq f(x)\frac{d}{dx}\)と同じ理屈。このような力を保存力という。保存力の仕事には経路に依らないという性質がある。 \[\int_{\boldsymbol{x}_0}^\boldsymbol{x}\boldsymbol{F}(\boldsymbol{x})\cdot d\boldsymbol{x}=\int_{\boldsymbol{x}_0}^\boldsymbol{x}-\nabla U(\boldsymbol{x})\cdot d\boldsymbol{x}\] スペースの関係で、関数である表記を省略します。 \[=\int_{\boldsymbol{x}_0}^\boldsymbol{x}-\left(\frac{\partial U}{\partial x}\boldsymbol{e}_x+\frac{\partial U}{\partial x}\boldsymbol{e}_y+\frac{\partial U}{\partial x}\boldsymbol{e}_z\right)\cdot d\boldsymbol{x}\] \[=\int_{\boldsymbol{x}_0}^\boldsymbol{x}-\left(\frac{\partial U}{\partial x}dx+\frac{\partial U}{\partial x}dy+\frac{\partial U}{\partial x}dz\right)\] かっこの中身は\(U(\boldsymbol{x})\)の前微分なので、 \[=\int_{\boldsymbol{x}_0}^{\boldsymbol{x}}-dU(\boldsymbol{x})=U(\boldsymbol{x}_0)-U(\boldsymbol{x})\] 以上から \[\int_{\boldsymbol{x}_0}^\boldsymbol{x}\boldsymbol{F}(\boldsymbol{x})\cdot d\boldsymbol{x}=U(\boldsymbol{x}_0)-U(\boldsymbol{x})\tag{5}\] 次に速度と仕事の関係について求めたいので運動方程式\(\boldsymbol{F}=m\frac{d\boldsymbol{v}}{dt}\)を代入して仕事を求めてみよう。 \[\boldsymbol{F}(\boldsymbol{x})\cdot d\boldsymbol{x}=m\frac{d\boldsymbol{v}}{dt}\cdot \frac{d\boldsymbol{x}}{dt}dt=m\frac{d\boldsymbol{v}}{dt}\cdot\boldsymbol{v}dt\] \[\frac{1}{2}m\frac{d(\boldsymbol{v}\cdot\boldsymbol{v})}{dt}dt=d\left(\frac{1}{2}m\boldsymbol{v}\cdot\boldsymbol{v}\right)=d\left(\frac{1}{2}mv^2\right)\] であるから、\(\boldsymbol{x}_0\)で物体の速度を\(\boldsymbol{v}_0\)、\(\boldsymbol{x}\)で物体の速度を\(\boldsymbol{v}\)とすると、 \[W_{\boldsymbol{x}_0\to\boldsymbol{x}}=\int_{\boldsymbol{x}_0}^{\boldsymbol{x}}\boldsymbol{F}(\boldsymbol{x})\cdot d\boldsymbol{x}\] \[=\int_{\boldsymbol{v}_0}^{\boldsymbol{v}}d\left(\frac{1}{2}mv^2\right)=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\] 上記の式と(5)式より、 \[\frac{1}{2}mv^2-\frac{1}{2}mv_0^2=U(\boldsymbol{x}_0)-U(\boldsymbol{x})\] \[\frac{1}{2}mv^2+U(\boldsymbol{x})=\frac{1}{2}mv_0^2+U(\boldsymbol{x}_0)\] となる。\(\frac{1}{2}mv^2\)を運動エネルギーと呼ぶことにしよう。

楽しい科学（理論）チャンネル

力学的エネルギー保存則