前回ベクトルの内積と外積についてやったが、今回はベクトルを関数として見ていこうと思う。 空間のある１点\(\boldsymbol{x}=(x\ y\ z)\)が決まると、その点での温度\(T(\boldsymbol{x})\)が１つに決まるようなのもはベクトルが１つ決まるとスカラーが１つ決まる関数である。放物運動している物体について、時間\(t\)がきまると、それに対応した位置\(\boldsymbol{x}(t)=(x(t)\ y(t)\ z(t))\)が１つに定まる。これはスカラーが１つ決まると、ベクトルが１つ決まる関数である。またある惑星が太陽から受ける万有引力\(\boldsymbol{F}_M\)は\(\boldsymbol{F}_M(\boldsymbol{x}(t))\)のように時間\(t\)によって位置\(\boldsymbol{x}\)が決まって、それによって\(\boldsymbol{F}_M\)が決まるという合成関数みたいなものも考えることができる。

　基本的にベクトルの割り算はないため、ベクトル\(\boldsymbol{A}=(A_x\ A_y\ A_z)\)をスカラー\(t\)で微分するということを考える。\(t\)の関数\(A_x(t)\)の微分は \[\frac{d}{dt}A_x(t)=\lim_{\varDelta t\to0}\frac{A_x(t+\varDelta t)-A_x(t)}{\varDelta t}\] である。ベクトル\(\boldsymbol{A}\)の各成分が\((A_x(t)\ A_y(t)\ A_z(t))\)のように\(t\)の関数の時\(\boldsymbol{A}=\boldsymbol{A}(t)\)のようにベクトルも\(t\)の関数のように表すことにする。 \[\boldsymbol{A}(t)=A_x(t)\boldsymbol{e}_x+A_y(t)\boldsymbol{e}_y+A_z(t)\boldsymbol{e}_z\] \(\boldsymbol{A}\)の\(t\)微分を \[\frac{d}{dt}\boldsymbol{A}(t):=\frac{dA_x(t)}{dt}\boldsymbol{e}_x+\frac{dA_y(t)}{dt}\boldsymbol{e}_y+\frac{dA_z(t)}{dt}\boldsymbol{e}_z\] のように計算することにする。３つの成分の微分を１つの微分で表せるので便利である。 \(t\)の関数\(\boldsymbol{A},\boldsymbol{B}\)ベクトル積、スカラー積の微分も示す。 \[\frac{d}{dt}(\boldsymbol{A}\cdot\boldsymbol{B})=\frac{d}{dt}(A_xB_x+A_yB_y+A_zB_z)\] \[=\frac{dA_x}{dt}B_x+A_x\frac{dB_x}{dt}+\frac{dA_y}{dt}B_y\] \[+A_y\frac{dB_y}{dt}+\frac{dA_z}{dt}B_z+A_z\frac{dB_z}{dt}\] \[=\frac{dA_x}{dt}B_x+\frac{dA_y}{dt}B_y+\frac{dA_z}{dt}B_z\] \[+A_x\frac{dB_x}{dt}+A_y\frac{dB_y}{dt}+A_z\frac{dB_z}{dt}\] \[=\frac{d\boldsymbol{A}}{dt}\cdot\boldsymbol{B}+\boldsymbol{A}\cdot\frac{d\boldsymbol{B}}{dt}\] 外積は\(z\)成分のみ示す。他の成分も同様に成り立つ。 \[\frac{d}{dt}[\boldsymbol{A}\times\boldsymbol{B}]_z=\frac{d}{dt}(A_xB_y-A_yB_x)\] \[=\frac{dA_x}{dt}B_y+A_x\frac{dB_y}{dt}-\frac{dA_y}{dt}B_x-A_y\frac{dB_x}{dt}\] \[=\frac{dA_x}{dt}B_y-\frac{dA_y}{dt}B_x+A_x\frac{dB_y}{dt}-A_y\frac{dB_x}{dt}\] \[=[\frac{d\boldsymbol{A}}{dt}\times\boldsymbol{B}]_z+[\boldsymbol{A}\times\frac{d\boldsymbol{B}}{dt}]_z\] ベクトル積、スカラー積でも\((fg)'=f'g+fg'\)のように微分してよいので覚えやすい！

　ベクトル\(\boldsymbol{A}\)が位置\(\boldsymbol{r}=(x\ y\ z)\)で決まる場合、\(\boldsymbol{A}=\boldsymbol{A}(x,y,z)=\boldsymbol{A}(\boldsymbol{r})\)をベクトル場という。下の図は \[\boldsymbol{A}(\boldsymbol{r})=\frac{x}{\sqrt{x^2+y^2}}\boldsymbol{e}_x+\frac{y}{\sqrt{x^2+y^2}}\boldsymbol{e}_y\] というベクトル場の例である。図は81箇所でベクトル\(\boldsymbol{A}\)を表示したが、実際は空間全体(この例の場合\((x\ y)=\boldsymbol{0}\)を除く)にベクトル\(\boldsymbol{A}(\boldsymbol{r})\)が定めてある。

このように、距離の２乗に反比例するベクトル場は万有引力や電場など、身の回りによくある。空間のある１点に対してスカラーが１つ決まる関数をスカラー場という。こちらは、気圧やポテンシャルエネルギーなどがある。

　1変数関数の積分は\(a=x_0\le\cdots\le x_i\le\cdots\le x_n=b\)の範囲で \[\int_a^bf(x)dx=\sum^{\infty}_{i=0}f(x_i)(x_{i+1}-x_{i})\] のように計算できる。これにより、距離の計算\(x=\int_a^b vdt\)やまっすぐな経路での仕事\(W=\int_a^bFdx\)が計算できるようになった。距離の計算では時間\(t\in ℝ\)のため、１変数の積分で十分である。しかし後者のような経路積分は直線の道とは限らない。途中で坂を上ったりカーブする経路での計算が必要であるため、3次元の経路\(C\)での積分を考える。一番自然な考えとして、経路\(C\in ℝ^3\)の上に短い線分\(\varDelta s\in ℝ^3\)を複数つなぎ\(C\)を線分\(\varDelta s\)で作る。\(i\)番目の線分\(\varDelta s_i\)を底辺として\(f(x_i,y_i,z_i)\)を高さとする長い長方形の和を線積分と定義しよう。 \[\int_Cf(x,y,z)ds:=\sum^{\infty}_{i=0}f(x_i,y_i\,z_i)\varDelta s_i\] この積分は次のようにも表せる。 \[\int_Cf(x,y,z)ds=\int_Cf(x,y,z)\frac{\partial s}{\partial x}dx\] \[+\int_Cf(x,y,z)\frac{\partial s}{\partial y}dy+\int_Cf(x,y,z)\frac{\partial s}{\partial z}dz\] 微小変位ベクトル\(d\boldsymbol{r}=(dx\ dy\ dz)\)、ベクトル場\(\boldsymbol{A}(\boldsymbol{r})=(f\frac{\partial s}{\partial x}\ f\frac{\partial s}{\partial y}\ f\frac{\partial s}{\partial z})\)とすると \[\int_Cf(x,y,z)ds=\int_C\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}\]のように表すこともできる。こちらは１変数関数の積分を線上での積分から経路による積分に拡張する方法だったが、ベクトル場がイメージできる場合は下のように覚えてもいいかもしれない。物理での線積分は下のパターンが多い。やってることは同じなので自分がわかりやすいほうを理解すればそれでよい。

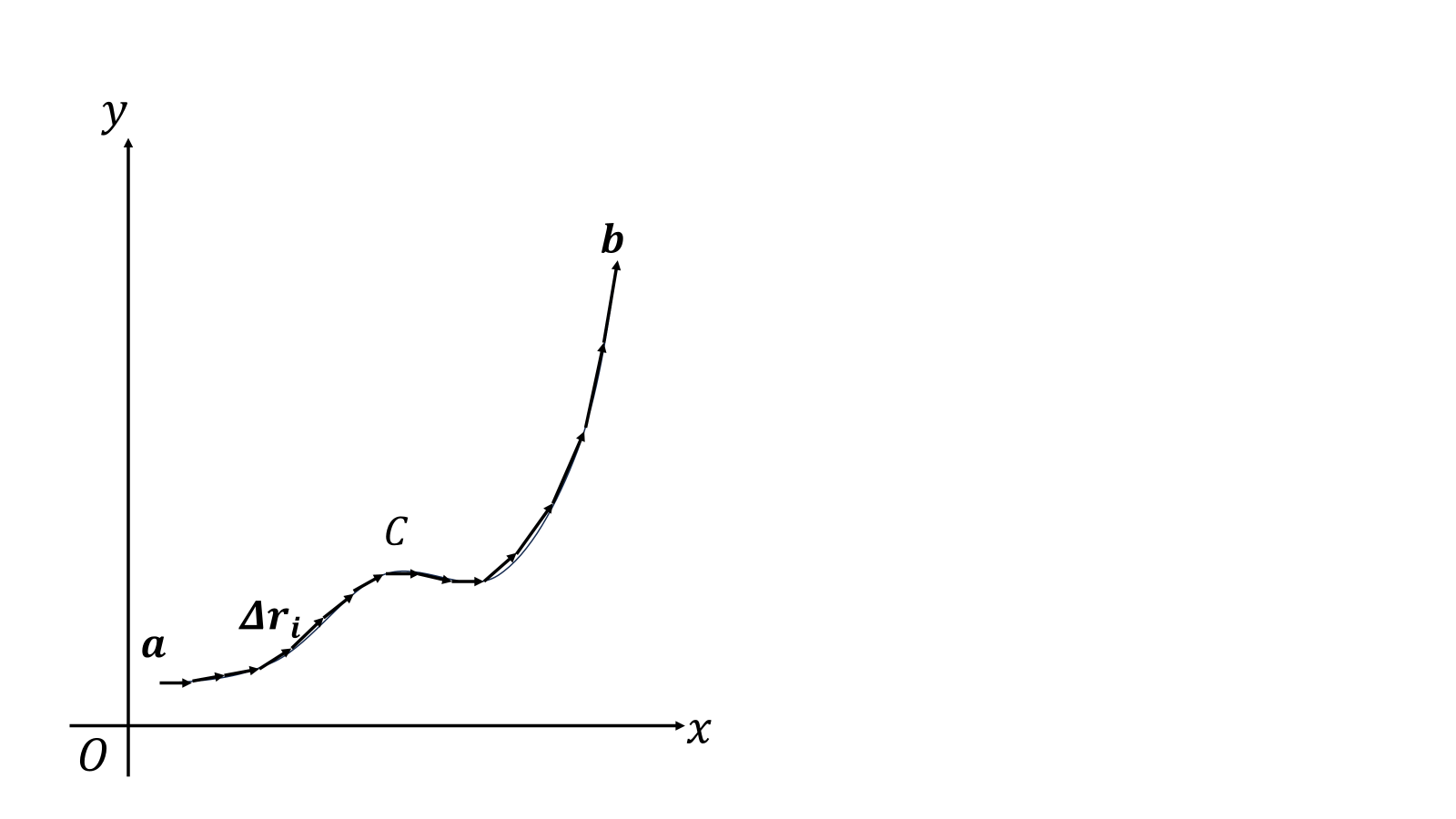
経路\(C\)上の任意の点を位置ベクトル\(\boldsymbol{r}\)で表すことができるとき、大まかに経路\(C\)は\(\{\boldsymbol{a}=\boldsymbol{r_0}\le\cdots\le\boldsymbol{r_i}\le\cdots\le\boldsymbol{r_n}=\boldsymbol{b}\}\)とあらわせる。\(n\to\infty\)でベクトル場\(\boldsymbol{A}(\boldsymbol{r})\)の線積分を \[\int_C\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}:=\sum_{i=0}^\infty\boldsymbol{A}(\boldsymbol{r_i})\cdot\varDelta\boldsymbol{r_i}\] とする。3次元のベクトル場であれば、 \[\int_C\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}=\int_CA_x(x,y,z)dx+\int_CA_y(x,y,z)dz\] \[+\int_CA_z(x,y,z)dz\] と表せる。３つの積分で計算が可能であるが、度の積分も積分する関数に他の変数が紛れていて、大抵の場合計算が難しいので、経路と直交するような座標軸をとるとか、\(\boldsymbol{r}=\boldsymbol{r}(t)\)のように媒介変数\(t\)を見つけて、 \[\int_C\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}=\int_{t_0}^tA_r(\boldsymbol{r}(t))\frac{dr}{dt}dt\] のような\(t\)の関数にして積分する場合が多い。自分で好きな経路を取ってもよければ簡単な経路を取るのも手である。１変数関数\(f(x)\)に原始関数\(F(x)\)が存在する場合\(dF(x)=f(x)dx\)と表せる。あるベクトル関数\(\boldsymbol{A}(\boldsymbol{r})\)が\(dF(x,y,z)=\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}\)を満たす関数\(F(x,y,z)\)があるとき、 十分に大きい数\(n\)を使い、 \[\int_CdF(\boldsymbol{r})=\sum_{i=0}^{n}(F(\boldsymbol{r}_{i+1})-F(\boldsymbol{r}_i))=F(\boldsymbol{r}_n)-F(\boldsymbol{r}_0)\] \[\int_CdF(\boldsymbol{r})=F(\boldsymbol{b})-F(\boldsymbol{a})\] この積分は経路\(C\)によらず始点\(\boldsymbol{a}\)と終点\(\boldsymbol{b}\)のみで決まる。関数\(F(x,y,z)\)は \[dF(x,y,z)=\frac{\partial F_x(x,y,z)}{\partial x}dx+\frac{\partial F_y(x,y,z)}{\partial y}dy+\frac{\partial F_z(x,y,z)}{\partial z}dz\]のように前微分されるので、 \[dF(x,y,z)=\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}\] \[=A_x(\boldsymbol{r})dx+A_y(\boldsymbol{r})dy+A_z(\boldsymbol{r})dz\] と係数を比較して、 \[A_x(\boldsymbol{r})=\frac{\partial F_x(x,y,z)}{\partial x}\] \[A_y(\boldsymbol{r})=\frac{\partial F_x(x,y,z)}{\partial y}\] \[A_z(\boldsymbol{r})=\frac{\partial F_x(x,y,z)}{\partial z}\] を満たす関数\(F(x,y,z)\)がある場合に限り \[\int_C\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}=F(\boldsymbol{b})-F(\boldsymbol{a})\] のように計算できる。