楽しい科学(理論)チャンネル
単振動
今回は実際に数字を入れて運動を見てみようの会である。記念すべき第1回は簡単な例で単振動をやる。数値解析は基本オイラー法(区分求積法)でやります!(簡単なので、)
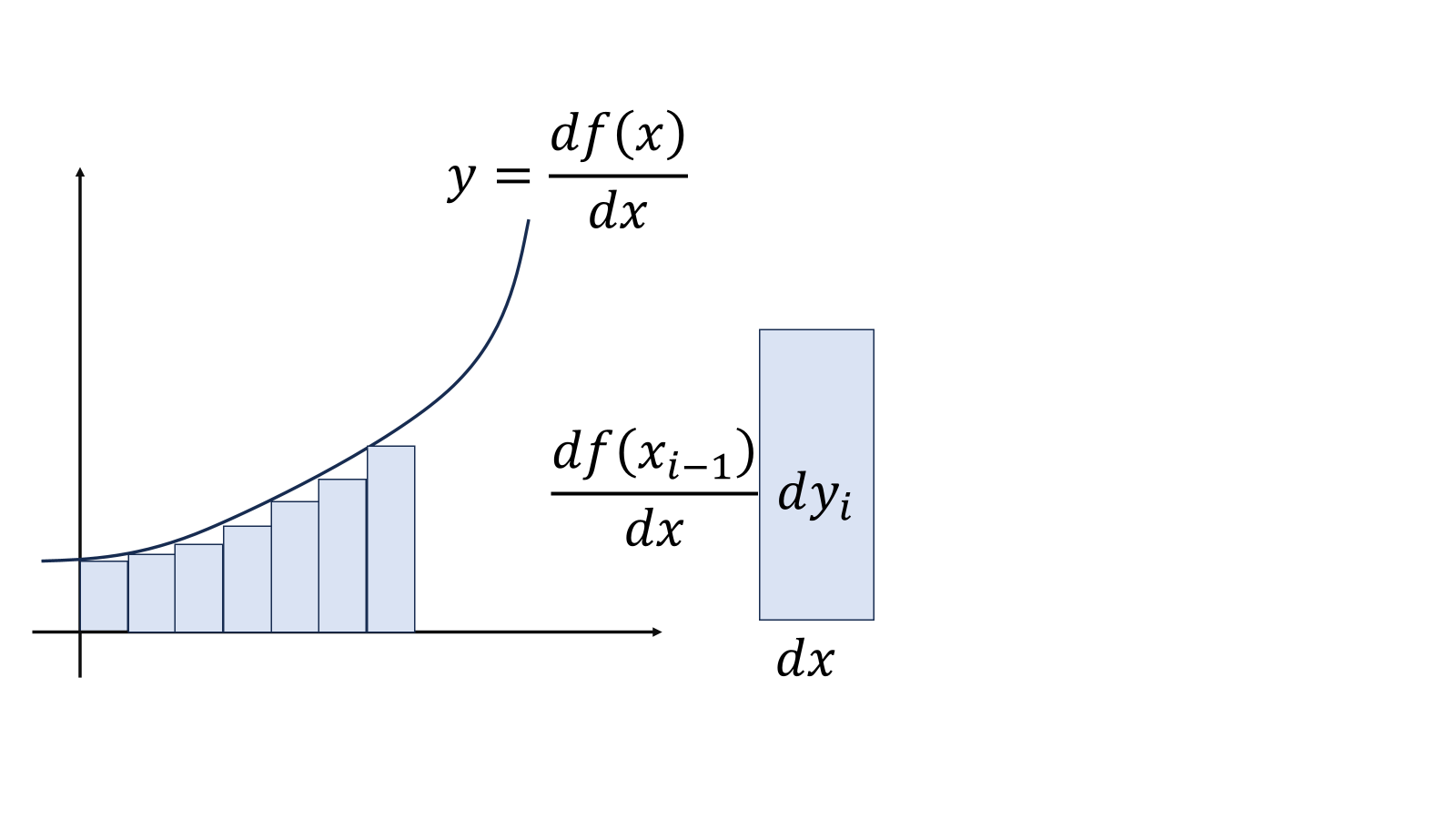
区分求積法は、面積\(y=f(x)\)を底辺\(dx\)高さ\(f(x_i)/dx\)の長方形の足し合わせでだいたい表せるというものである。左から数えて\(i\)番目の長方形の面積は\(dy_i=\frac{f(x_{i-1})}{dx}dx\)なので、
\[y\simeq \sum_i\frac{f(x_i)}{dx}dx\]
となる。ここで扱う微小量\(dx\)は限りなく小さい値ではなく、ある程度小さい値であれば大丈夫。ただし、小さいほうが正確な\(y\)が求められる。単振動の方程式は
\[\frac{d^2x}{dt^2}=-\omega^2x\]
人間であれば方程式を解いて\(x=x_0\cos\omega t+\frac{v_0}{\omega}\sin\omega t\)とするところだが
微小時間\(dt\)というものを用意して、javascriptに
\[\omega,\ v_0,\ x_0=const.\]
\[v_i=v_{i-1}-w^2x_{i-1}dt\]
\[x_i=x_{i-1}+v_idt\]
の手順で計算してもらおう。定数は変えられるようにしたので、変えて遊んでみてほしい。全角だとうまくいかないので定数は半角でお願いします。
初期位置\([x_0]=\mathrm{m}\)
初期速度\([v_0]=\mathrm{m\ s^{-1}}\)
角振動数\([\omega]=\mathrm{rad\ s^{-1}}\)
オイラー法では、長方形を並べても隙間の部分ができてしまう。オイラー法がどれだけ現実に近い動きを再現できているか、単振動の解は\(x=a\cos\omega t\)の形で書けるので、これと上で計算した\(x_i\)を並べて見比べてみよう。
結果がこちら、\(\omega=8\ \mathrm{rad\ s^{-1}}\)でやった結果である。白丸が本物の単振動で黒丸が近似した\(x_i\)である。実際の単振動より初速が早いという印象である。\(\omega=1\ \mathrm{rad\ s^{-1}}\)では肉眼で差が見られなかった。オイラー法でも十分よい近似といえる。htmlが使え自分でも試してみたいという方はとてもお粗末なコードだが、参考にしてみてほしい。以下のコードをhtmlファイルの<body></body>の中にコピペでできるはず。
<div>
初期位置
</div>
<input id="input1">
<div>
初期速度
</div>
<input id="input2">
<div>
角振動数
</div>
<input id="input3">
<div>
<button id="button1">
スタート
</button>
</div>
<canvas id="canvas1"></canvas>
<script>
let xin = document.getElementById("input1");
xin.value = 3;
let vin = document.getElementById("input2");
vin.value = 0;
let omega = document.getElementById("input3");
omega.value = 1;
let but1 = document.getElementById("button1")
let width = 600;
let height = 300;
let canvas1 = document.getElementById("canvas1");
let c1 = canvas1.getContext("2d");
canvas1.width = width;
canvas1.height = height;
let cn=c1;
let xo = 50;
let yo = 250;
let x = 40*xin.value;
let v = 40*vin.value;
let ome = 1*omega.value;
let dt=0.01;
let setI = setInterval(()=>{
cn.clearRect(0,0,width,height);
cn.beginPath();
cn.moveTo(xo,yo);
cn.lineTo(xo+400,yo);
cn.stroke();
for (i=0;i<11;i++) {
cn.beginPath();
cn.moveTo(xo+i*40,yo);
cn.lineTo(xo+i*40,yo+10);
cn.stroke();
cn.font = "20px 'Alial'";
cn.fillText(i-5,xo+40*i,yo+20);
}
cn.beginPath();
cn.arc(xo+200+x,yo-80,4,0,Math.PI*2);
cn.fill();
cn.save();
cn.beginPath();
cn.setLineDash([3, 5]);
cn.moveTo(xo,yo-80);
cn.lineTo(xo+400,yo-80);
cn.stroke();
cn.restore();
v = v - ome**2*x*dt;
x = x + v*dt;
},10);
but1.addEventListener("click",()=>{
xin = document.getElementById("input1");
vin = document.getElementById("input2");
omega = document.getElementById("input3");
x = 40*xin.value;
v = 40*vin.value;
ome = 1*omega.value;
});
</script>
