楽しい科学(理論)チャンネル
振り子
今回は、実際に数値を入れて運動を見ようの第3弾!
振り子である。実はこちらも一般解はそう簡単に求められない。これも数値解析の出番だ。糸のたわみのないものを仮定する。糸というよりは棒である。
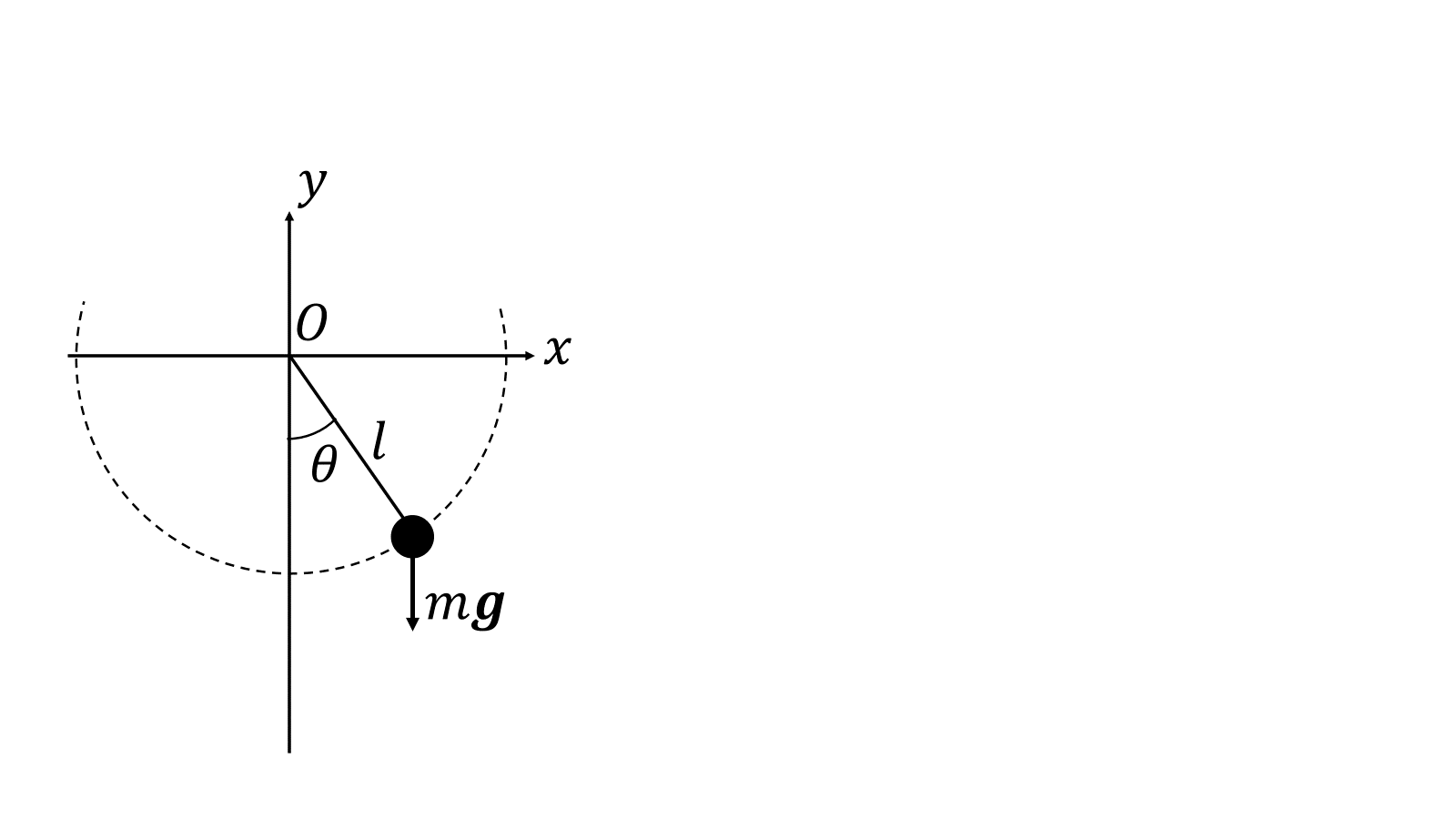
長さ\(l\)の糸からの張力を\(T_{string}\)とすると、物体の運動方程式は
\[m\frac{d^2x}{dt^2}=-T_{string}\sin\theta\]
\[m\frac{d^2y}{dt^2}=T_{string}\cos\theta-mg\]
\(x\)成分に\(\cos\theta\)、\(y\)成分に\(\sin\theta\)を掛けて2つの式を足すと、\(T_{string}\)を消去できる。
\[\cos\theta\ m\frac{d^2x}{dt^2}+\sin\theta\ m\frac{d^2y}{dt^2}=-mg\sin\theta\tag{1}\]
直交座標では難しそうなので\((x,y)=(l\sin\theta,-l\cos\theta)\)としよう。
\[\begin{pmatrix}\dot x\\\dot y\end{pmatrix}=\begin{pmatrix}l\cos\theta\ \dot\theta\\l\sin\theta\ \dot\theta\end{pmatrix}\]
\[\begin{pmatrix}\ddot x\\\ddot y\end{pmatrix}=\begin{pmatrix}-l\sin\theta\ \dot\theta^2+l\cos\theta\ \ddot\theta\\l\cos\theta\ \dot\theta^2+l\sin\theta\ \ddot\theta\end{pmatrix}\]
これを(1)式に代入すると、\(\dot\theta\)の項がなくなる。
\[ml\frac{d^2\theta}{dt^2}=-mg\sin\theta\]
\[\frac{d^2\theta}{dt^2}=-\frac{g}{l}\sin\theta\]
シンプルな形になったのでこれで、数値解析をやってみる。
\[\theta_0,\ \dot\theta_0,\ l,\ g=const.\]
\[\dot\theta_i=\dot\theta_{i-1}-\frac{g}{l}\sin\theta_{i-1} dt\]
\[\theta_i=\theta_{i-1}+\dot\theta_{i-1}dt\]
\[(x_i,y_i)=(l\sin\theta_i,-l\cos\theta_i)\]
このように計算していただこう。
初期角度\([\theta_0]=\mathrm{rad}\)
初期角速度\([\dot\theta_0]=\mathrm{rad\ s^{-1}}\)
糸の長さ\([l]=\mathrm{m}\)
重力加速度\([g]=\mathrm{m\ s^{-2}}\)
\(\sin\theta\)を原点でテイラー展開すると、\[\sin\theta=\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\cdots\]
となる。\(\theta\)が十分に小さいとき\(\theta^3/3!\)以降の項を無視して、
\[\frac{d^2\theta}{dt^2}\simeq\frac{g}{l}\theta\]
と単振動の微分方程式になる。単振動とみれば各振動数\(\omega=2\pi/T=g/l\)なので、糸を長くすると、周期運動が遅くなり、重力が大きい所では周期運動が早くなることがわかるだろう。\(\theta=3\)とかにして運動を見てみてほしい。単振動で近似できないのがみてわかる。初期角速度を大きくしていて1回転する振り子を見るのも面白い。今回使ったコードを最後に載せておく。
<div>
糸の長さ
重力加速度
</div>
<input id="input3">
<input id="input4">
<div>
<button id="button1">
スタート
</button>
</div>
<canvas id="canvas1">
<script>
//inputを取得てきとーに名前を定義してあげる。
let theint = document.getElementById("input1");
let vthint = document.getElementById("input2");
let lstrin = document.getElementById("input3");
let gravac = document.getElementById("input4");
// inputに初期値を代入
theint.value = 0.1;
vthint.value = 0;
lstrin.value = 2;
gravac.value = 9.8;
//buttonを取得、名前を付ける。
let but1 = document.getElementById("button1");
//canvasAPIのお約束事
let width = 600;
let height = 600;
let canvas1 = document.getElementById("canvas1");
let c1 = canvas1.getContext("2d");
canvas1.width = width;
canvas1.height = height;
let cn=c1;
//定数
let xo = 50;
let yo = 550;
let dt = 0.01;
//inputから拾った文字列を1を掛けて数にする。
let th = 1*theint.value;
let vth = 1*vthint.value;
let ls = 1*lstrin.value;
let g = 1*gravac.value;
let x = ls*Math.sin(th);
let y = -ls*Math.cos(th);
//setInervalでcanvasを10ms間隔で更新
let setI = setInterval(()=>{
//10ms前の描写をクリア
cn.clearRect(0,0,width,height);
//グラフの軸、目盛り
cn.beginPath();
cn.moveTo(xo,yo);
cn.lineTo(xo+400,yo);
cn.stroke();
cn.beginPath();
cn.moveTo(xo,yo);
cn.lineTo(xo,yo-400);
cn.stroke();
for (i=0;i<11;i++) {
cn.beginPath();
cn.moveTo(xo,yo-i*40);
cn.lineTo(xo-10,yo-i*40);
cn.stroke();
cn.beginPath();
cn.moveTo(xo+i*40,yo);
cn.lineTo(xo+i*40,yo+10);
cn.stroke();
cn.font = "20px 'Alial'";
cn.fillText(i-5,xo+40*i,yo+20);
cn.fillText(i-5,xo-40,yo-40*i);
};
//物体arc(円)を使う。
cn.beginPath();
cn.arc(xo+200+40*x,yo-200+40*y,4,0,Math.PI*2);
cn.fill();
//糸
cn.beginPath();
cn.moveTo(xo+200,yo-200);
cn.lineTo(xo+200+40*x,yo-200+40*y);
cn.stroke();
//点線
cn.save();
cn.setLineDash([3, 5]);
cn.beginPath();
cn.moveTo(xo+200,yo);
cn.lineTo(xo+200,yo-400);
cn.stroke();
cn.beginPath();
cn.moveTo(xo,yo-200);
cn.lineTo(xo+400,yo-200);
cn.stroke();
cn.restore();
// 次の描写時に位置を決めるための計算
vth = vth - g/ls*Math.sin(th)*dt;
th = th + vth*dt;
x = ls*Math.sin(th);
y = ls*Math.cos(th);
},10);
// ボタンを押すとinputの値を再取得する仕組み
but1.addEventListener("click",()=>{
theint = document.getElementById("input1");
vthint = document.getElementById("input2");
lstrin = document.getElementById("input3");
gravac = document.getElementById("input4");
th = 1*theint.value;
vth = 1*vthint.value;
ls = 1*lstrin.value;
g = 1*gravac.value;
x = ls*Math.sin(th);
y = -ls*Math.cos(th);
});
<\script>
