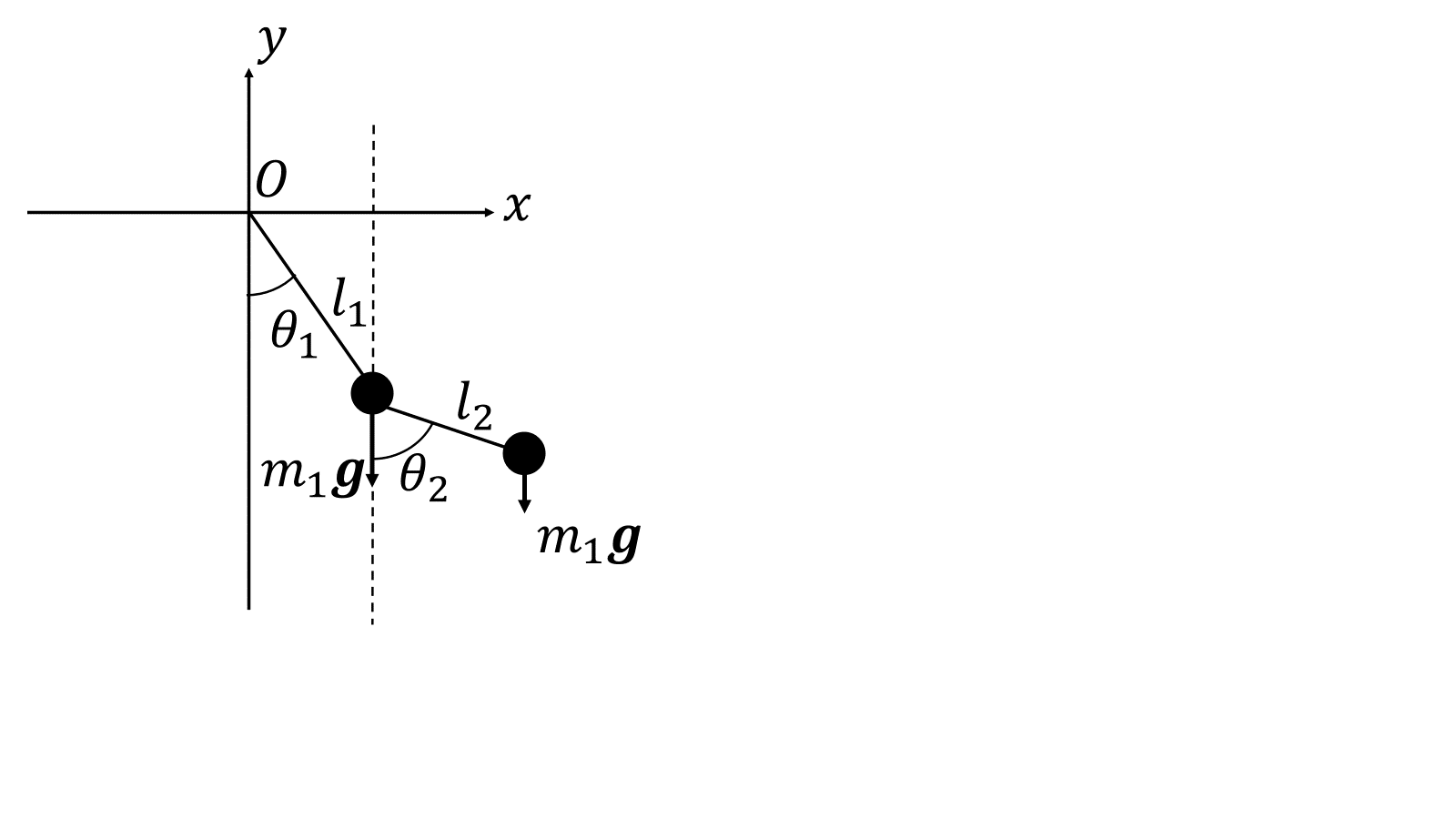
今回は2物体系の数値解析。万有引力も太陽を原点に固定しないで相互作用を受ける物体を3つに増やす等でかなり複雑になると思う。ここでは振り子に振り子が付いている2重振り子をやる。式の意味とかを知ることには意味があるが、計算は面白いことが何もないのでw読み飛ばしましょう。
振り子1の運動方程式を立てる。
\[m_1\begin{pmatrix}\ddot x_1\\\ddot y_1\end{pmatrix}=\begin{pmatrix}-T_1\sin\theta_1+T_2\sin\theta_2\\T_1\cos\theta_1-T_2\cos\theta_2-m_1g\end{pmatrix}\tag{1}\]
振り子2の運動方程式は、
\[m_2\begin{pmatrix}\ddot x_2\\\ddot y_2\end{pmatrix}=\begin{pmatrix}-T_2\sin\theta_2\\T_2\cos\theta_2-m_2g\end{pmatrix}\tag{2}\]
(2)式の\(x\)成分\(\times\cos\theta_2+y\)成分\(\times\sin\theta_2\)から\(T_2\)を消去できる。
\[m_2 \ddot x_2\cos\theta_2+m_2\ddot y_2\sin\theta_2=-m_2g\sin\theta_2\]
\[\ddot x_2\cos\theta_2+\ddot y_2\sin\theta_2=-g\sin\theta_2\tag{3}\]
(1)式\(+\)(2)式で\(T_2\)を消去する。
\[\begin{pmatrix}m_1\ddot x_1+m_2\ddot x_2\\m_1\ddot y_1+m_2\ddot y_2\end{pmatrix}=\begin{pmatrix}-T_1\sin\theta_1\\T_1\cos_1\theta-m_1g-m_2g\end{pmatrix}\]
この式の\(x\)成分\(\times\cos\theta_1+\)\(y\)成分\(\times\sin\theta_1\)
\[(m_1\ddot x_1+m_2\ddot x_2)\cos\theta_1+(m_1\ddot y_1+m_2\ddot y_2)\sin\theta_1\]
\[=-(m_1+m_2)g\sin\theta_1\tag{4}\]
1つ目の振り子の位置\((x_1,y_1)\)を時間で微分して加速度を求める。
\[\begin{pmatrix}\dot x_1\\\dot y_1\end{pmatrix}=\begin{pmatrix}l_1\cos\theta_1\ \dot\theta_1\\l_1\sin\theta_1\ \dot\theta_1\end{pmatrix}\]
\[\begin{pmatrix}\ddot x_1\\\ddot y_1\end{pmatrix}=\begin{pmatrix}-l_1\sin\theta_1\ \dot\theta_1^2+l_1\cos\theta_1\ \ddot\theta_1\\l_1\cos\theta_1\ \dot\theta_1^2+l_1\sin\theta_1\ \ddot\theta_1\end{pmatrix}\]
次に振り子に繋がっている振り子(2個目の振り子)の位置を\((x_2,y_2)\)としてこちらも加速度を求める。
\[\begin{pmatrix}x_2\\y_2\end{pmatrix}=\begin{pmatrix}l_1\sin\theta_1+l_2\sin\theta_2\\-l_1\cos\theta_1-l_2\cos\theta_2\end{pmatrix}\]
\[\begin{pmatrix}\ddot x_2\\\ddot y_2\end{pmatrix}=\begin{pmatrix}-l_1\sin\theta_1\ \dot\theta_1^2+l_1\cos\theta_1\ \ddot\theta_1-l_2\sin\theta_2\ \dot\theta_2^2+l_2\cos\theta_2\ \ddot\theta_1\\l_1\cos\theta_1\ \dot\theta_1^2+l_1\sin\theta_1\ \ddot\theta_1+l_2\cos\theta_2\ \dot\theta_2^2+l_2\sin\theta_2\ \ddot\theta_2\end{pmatrix}\]
これらを(3)式、(4)式に代入する。\(\sin\theta=s\theta,\ \cos\theta=c\theta,\ m_1+m_2=M\)とさせて下さい。まずは(3)式、
\[\ddot x_2c\theta_2+\ddot y_2s\theta_2=-gs\theta_2\]
\(\theta_1,\theta_2\)で表すと、
\[(-l_1s\theta_1\dot{\theta}_1^2+l_1c\theta_1\ddot{\theta}_1-l_2s\theta_2\dot{\theta}_2^2+l_2c\theta_2\ddot{\theta}_2)c\theta_2\]
\[+(l_1c\theta_1\dot{\theta}_1^2+l_1s\theta_1\ddot{\theta}_1+l_2c\theta_2\dot{\theta}_2^2+l_2s\theta_2\ddot{\theta}_2)s\theta_2=-gs\theta_2\]
整理すると、
\[c(\theta_1-\theta_2)l_1\ddot{\theta}_1+l_2\ddot{\theta}_2=-gs\theta_2+s(\theta_1-\theta_2)l_1\dot{\theta}_1^2\tag{5}\]
(4)式は次のようになる。
\[(m_1\ddot x_1+m_2\ddot x_2)c\theta_1+(m_1\ddot y_1+m_2\ddot y_2)s\theta_1=-Mgs\theta_1\]
\(\theta_1,\theta_2\)で表すと、
\[m_1(-l_1s\theta_1\dot{\theta}_1^2+l_1c\theta_1\ddot{\theta}_1)c\theta_1\]
\[+m_2(-l_1s\theta_1\dot{\theta}_1^2+l_1c\theta_1\ddot{\theta}_1-l_2s\theta_2\dot{\theta}_2^2+l_2c\theta_2\ddot{\theta}_2)c\theta_1\]
\[m_1(l_1c\theta_1\dot{\theta}_1^2+l_1s\theta_1\ddot{\theta}_1)s\theta_1\]
\[+m_2(l_1c\theta_1\dot{\theta}_1^2+l_1s\theta_1\ddot{\theta}_1+l_2c\theta_2\dot{\theta}_2^2+l_2s\theta_2\ddot{\theta}_2)s\theta_1=-Mgs\theta_1\]
\[Ml_1\ddot{\theta}_1+c(\theta_1-\theta_2)m_2l_2\ddot{\theta}_2=-Mgs\theta_1-s(\theta_1-\theta_2)m_2l_2\dot{\theta}_2^2\tag{6}\]
(5)(6)式から\(\ddot{\theta}_1,\ddot{\theta}_2\)を求めるため連立方程式を解いてもよいのだが、せっかくコンピューターで解くので楽をしよう。\(2\times2\)行列\(A\)、ベクトル\(\ddot{\boldsymbol{\theta}},\boldsymbol{d}\)を次のようにする。
\[A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}=\begin{pmatrix}c(\theta_1-\theta_2)l_1&l_2\\Ml_1&c(\theta_1-\theta_2)m_2l_2\end{pmatrix},\ \ddot{\boldsymbol{\theta}}=\begin{pmatrix}\ddot\theta_1\\\ddot\theta_2\end{pmatrix}\]
\[\boldsymbol{d}=\begin{pmatrix}d_1\\d_2\end{pmatrix}=\begin{pmatrix}-gs\theta_2+s(\theta_1-\theta_2)l_1\dot\theta_1^2\\-Mgs\theta_1-s(\theta_1-\theta_2)m_2l_2\dot{\theta}_2^2\end{pmatrix}\]
後の計算は人間には厳しいので、コンピューターにやってもらう。運動の計算は今回もオイラー法をつかう。
\[m_1,m_2,l_1,l_2,\theta_{1}(t_0),\theta_{2}(t_0),\dot{\theta}_1(t_0),\dot{\theta}_1(t_0)=const.\]
\[\ddot{\boldsymbol{\theta}}=A^{-1}\boldsymbol{d}\]
\[\dot{\theta}_\nu(t_i)=\dot{\theta}_\nu(t_{i-1})+\ddot{\theta}_\nu(t_{i-1})dt\ \ (\nu=1,2)\]
\[\theta_\nu(t_i)=\theta_\nu(t_{i-1})+\dot{\theta_\nu}(t_{i-1})dt\ \ (\nu=1,2)\]
\[\begin{pmatrix}x_1(t_i)\\y_1(t_i)\end{pmatrix}=\begin{pmatrix}l_1\sin\theta_1(t_i)\\-l_1\cos\theta_1(t_i)\end{pmatrix}\]
\[\begin{pmatrix}x_2(t_i)\\y_2(t_i)\end{pmatrix}=\begin{pmatrix}l_1\sin\theta_1(t_i)+l_2\sin\theta_2(t_i)\\-l_1\cos\theta_1(t_i)-l_2\cos\theta_2(t_i)\end{pmatrix}\]
のようにして運動を求める。
振り子1
質量\(\ \mathrm{kg}\)
糸の長さ\(\ \mathrm{m}\)
角度\(\ \mathrm{rad}\)
角速度\(\ \mathrm{rad\ s^{-1}}\)
振り子2
質量\(\ \mathrm{kg}\)
糸の長さ\(\ \mathrm{m}\)
角度\(\ \mathrm{rad}\)
角速度\(\ \mathrm{rad\ s^{-1}}\)
作っての感想。振り子の計算がとにかく大変だった。今回連立方程式をjavascriptに解いてもらった。そのため連立方程式の解の分母の部分\((\det A=0)\)付近にならないような数値の範囲内で遊んでほしい。入れた数値によってはうまく動いてくれないこともある。オイラー法だと明らかに運動が減衰しているように見えることもあるし極端な運動だと精度もさがるのかな。重りの質量や、角度をを\(0.1\)変えたりするだけでも全く別の運動になる。複数の物体が絡む運動は複雑なのだ。コードは以下に貼っておく。
<div>
振り子1
</div>
<div>
質量
糸の長さ
角度
角速度
</div>
<input id="input1">
<input id="input2">
<input id="input3">
<input id="input4">
<div>
振り子2
</div>
<div>
質量
糸の長さ
角度
角速度
</div>
<input id="input5">
<input id="input6">
<input id="input7">
<input id="input8">
<div>
<button id="button1">スタート</button>
</div>
<script>
//inputのを取得
let inputs = [];
let consta = [2, 2, 2, 0, 1, 1, 1, 0];
for (i = 1; i < 9; i ++) {
inputi = "input" + i;
inputi = document.getElementById(inputi);
inputs.push(inputi);
//inputに初期値を入れる。
inputi.value = consta[i-1];
};
//buttonを取得、名前を付ける。
let but1 = document.getElementById("button1");
//canvasAPIのお約束事
let width = 600;
let height = 600;
let canvas1 = document.getElementById("canvas1");
let c1 = canvas1.getContext("2d");
canvas1.width = width;
canvas1.height = height;
let cn=c1;
//三角関数を短くする。
let sin = (x) => {return Math.sin(x)};
let cos = (x) => {return Math.cos(x)};
//inputの文字列を取得して、数字にする。
let mas1 = 1*inputs[0].value;
let leg1 = 1*inputs[1].value;
let the1 = 1*inputs[2].value;
let vth1 = 1*inputs[3].value;
let mas2 = 1*inputs[4].value;
let leg2 = 1*inputs[5].value;
let the2 = 1*inputs[6].value;
let vth2 = 1*inputs[7].value;
//定数
let xo = 50;
let yo = 550;
let dt = 0.01;
let x1 = leg1*sin(the1);
let y1 = -leg1*cos(the1);
let x2 = x1 + leg2*sin(the2);
let y2 = x1 - leg2*cos(the2);
let cos12 = 0;
let sin12 = 0;
let a11 = 0;
let a12 = leg2;
let a21 = (mas1+mas2)*leg1;
let a22 = 0;
let detA = 0;
let d1 = 0;
let d2 = 0;
let setI = setInterval(()=>{
//10ms前の描写をクリア
cn.clearRect(0,0,width,height);
//グラフの軸、目盛り
cn.beginPath();
cn.moveTo(xo,yo);
cn.lineTo(xo+400,yo);
cn.stroke();
cn.beginPath();
cn.moveTo(xo,yo);
cn.lineTo(xo,yo-400);
cn.stroke();
for (i = 0; i < 11; i++) {
cn.beginPath();
cn.moveTo(xo,yo-i*40);
cn.lineTo(xo-10,yo-i*40);
cn.stroke();
cn.beginPath();
cn.moveTo(xo+i*40,yo);
cn.lineTo(xo+i*40,yo+10);
cn.stroke();
cn.font = "20px 'Alial'";
cn.fillText(i-5,xo+40*i,yo+20);
cn.fillText(i-5,xo-40,yo-40*i);
};
//振り子1重り
cn.beginPath();
cn.arc(xo+200+40*x1,yo-200-40*y1,4,0,Math.PI*2);
cn.fill();
//振り子1糸
cn.beginPath();
cn.moveTo(xo+200,yo-200);
cn.lineTo(xo+200+40*x1,yo-200-40*y1);
cn.stroke();
//振り子2重り
cn.beginPath();
cn.arc(xo+200+40*x2,yo-200-40*y2,4,0,Math.PI*2);
cn.fill();
//振り子2糸
cn.beginPath();
cn.moveTo(xo+200+40*x1,yo-200-40*y1);
cn.lineTo(xo+200+40*x2,yo-200-40*y2);
cn.stroke();
//点線
cn.save();
cn.setLineDash([3, 5]);
cn.beginPath();
cn.moveTo(xo+200,yo);
cn.lineTo(xo+200,yo-400);
cn.stroke();
cn.beginPath();
cn.moveTo(xo,yo-200);
cn.lineTo(xo+400,yo-200);
cn.stroke();
cn.restore();
// 次の描写時の位置を決めるための計算
cos12 = cos(the1-the2);
sin12 = sin(the1-the2);
a11 = cos12*leg1;
a22 = cos12*mas2*leg2;
detA = a11*a22 - a12*a21;
d1 = -9.8*sin(the2) + sin12*leg1*vth1**2;
d2 = -(mas1+mas2)*9.8*sin(the1)
- sin12*mas2*leg2*vth2**2;
vth1 = vth1 + (a22*d1-a12*d2)/detA*dt;
vth2 = vth2 + (-a21*d1+a11*d2)/detA*dt;
the1 = the1 + vth1*dt;
the2 = the2 + vth2*dt;
x1 = leg1*sin(the1);
y1 = -leg1*cos(the1);
x2 = x1 + leg2*sin(the2);
y2 = y1 - leg2*cos(the2);
console.log(a11)
},10);
// ボタンを押すとinputの値を再取得する仕組み
but1.addEventListener("click",()=>{
inputs = [];
for (i = 1; i < 9; i ++) {
inputi = "input" + i;
inputi = document.getElementById(inputi);
inputs.push(inputi);
};
mas1 = 1*inputs[0].value;
leg1 = 1*inputs[1].value;
the1 = 1*inputs[2].value;
vth1 = 1*inputs[3].value;
mas2 = 1*inputs[4].value;
leg2 = 1*inputs[5].value;
the2 = 1*inputs[6].value;
vth2 = 1*inputs[7].value;
});
</script>