楽しい科学(理論)チャンネル
3体問題 初期値敏感性
今回は3つの天体があるときの天体の軌跡を見てみよう!
ただ自由に天体たちを運動させると物体系の重心が画面から遠ざかって見えなくなってしまうので、天体を1つだけ原点に固定して、他の2つの天体がどのような軌跡を描くか見ていきたい。
3名の選手入場!エントリーナンバー1、太陽(質量\(M\)、位置ベクトル\(\boldsymbol{x}_M=(0,0,0)\))、エントリーナンバー2、惑星1(質量\(m_1\)、位置ベクトル\(\boldsymbol{x}_1=(x_1,y_1,z_1)\))、エントリーナンバー3、惑星2(質量\(m_2\)、位置ベクトル\(\boldsymbol{x}_1=(x_2,y_2,z_2)\))
惑星1の運動方程式は
\[m_1\ddot{\boldsymbol{x}}_1=-G\frac{Mm_1\boldsymbol{x}_1}{|\boldsymbol{x}_1|^{\frac{3}{2}}}-G\frac{m_1m_2(\boldsymbol{x}_1-\boldsymbol{x}_2)}{|\boldsymbol{x}_1-\boldsymbol{x}_2|^{\frac{3}{2}}}\]
惑星2の運動方程式は
\[m_2\ddot{\boldsymbol{x}}_2=-G\frac{Mm_2\boldsymbol{x}_2}{|\boldsymbol{x}_2|^{\frac{3}{2}}}-G\frac{m_1m_2(\boldsymbol{x}_2-\boldsymbol{x}_1)}{|\boldsymbol{x}_2-\boldsymbol{x}_1|^{\frac{3}{2}}}\]
ベクトルを使うとすっきりした形である。
今回もオイラー法を使う。惑星1の位置ベクトルは次のようにして計算してもらう。
\[\boldsymbol{x}_1(t_0),\dot{\boldsymbol{x}}_1(t_0)=\boldsymbol{const.},\ M,m_1,m_2,G=const.\]
\[\dot{\boldsymbol{x}}_1(t_i)=-G\frac{M\boldsymbol{x}_1(t_{i-1})}{|\boldsymbol{x}_1(t_{i-1})|^{\frac{3}{2}}}\varDelta t-G\frac{m_2(\boldsymbol{x}_1(t_{i-1})-\boldsymbol{x}_2(t_{i-1}))}{|\boldsymbol{x}_1(t_{i-1})-\boldsymbol{x}_2(t_{i-1})|^{\frac{3}{2}}}\varDelta t\]
\[\boldsymbol{x}_1=\boldsymbol{x}_1(t_{i-1})+\dot{\boldsymbol{x}}_1(t_{i-1})\varDelta t\]
惑星2についても同様だ。(添え字の1と2を変えるだけ。)
太陽 質量
惑星1 質量
初期座標\(x,y,z\)
惑星2 質量
初期座標\(x,y,z\)
太陽を白、惑星1を赤、惑星2を青にした。こちらも数値を変えることができるので、いろいろ遊べる。惑星同士を逆向きに回転させれば本当に動きが読めない。一方の質量を極端に小さくして、同じ軌道に乗せれば地球と月のような運動も観察できる。

図1 パラメータ(input)右から上順に、2,1,1,-2,0,-0.3,0,0,1,-1,2,0.3,0,0での結果、青色の四角が0 month,緑色の四角が100 monthの位置を示す。
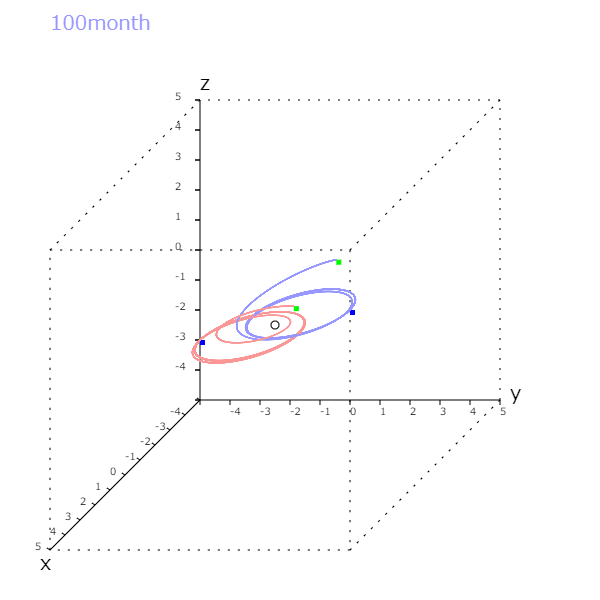
図2 図1の惑星のy座標を-2から-2.001でスタートしたものである。初めはたった、0.001の差であったが100 monthの時間経過で全く別の場所についてしまった。1物体の一様な重力場の運動などではこのようなことがないのだが、複数の物体があると初期値の少しの違いが後に大きな違いになることもあるのだ。今回使ったコードを載せておこう。
<div>太陽 質量</div>
<div>
<input>
</div>
<div>
惑星1 質量
</div>
<div>
<input>
</div>
<div>初期座標</div>
<div>
<input>
<input>
<input>
</div>
<div>
初速度
</div>
<div>
<input>
<input>
<input>
</div>
<div>
惑星2 質量
</div>
<div>
<input>
</div>
<div>初期座標</div>
<div>
<input>
<input>
<input>
</div>
<div>
初速度
</div>
<div>
<input>
<input>
<input>
</div>
<div>
<button id="button1">スタート</button>
</div>
<canvas id="canvas1"></canvas>
<script>
//inputのを取得
let inputs = document.getElementsByTagName("input");
let consta = [
2,
0.5,
0, 3, 2,
0, 0, -0.2,
0.1,
0, 3, 1,
0, 0.2, -0.2];
//初期値の代入
for (i = 0; i < 15; i ++) {
inputs[i].value = consta[i]
};
//buttonを取得、名前を付ける。
let but1 = document.getElementById("button1");
//canvasAPIのお約束事
let width = 600;
let height = 600;
let canvas1 = document.getElementById("canvas1");
let c1 = canvas1.getContext("2d");
canvas1.width = width;
canvas1.height = height;
let cn=c1;
//inputの文字列を取得して、数字にする。
let mas0 = 1*inputs[0].value;
let mas1 = 1*inputs[1].value;
let x1 = 1*inputs[2].value;
let y1 = 1*inputs[3].value;
let z1 = 1*inputs[4].value;
let vx1 = 1*inputs[5].value;
let vy1 = 1*inputs[6].value;
let vz1 = 1*inputs[7].value;
let mas2 = 1*inputs[8].value;
let x2 = 1*inputs[9].value;
let y2 = 1*inputs[10].value;
let z2 = 1*inputs[11].value;
let vx2 = 1*inputs[12].value;
let vy2 = 1*inputs[13].value;
let vz2 = 1*inputs[14].value;
let d12 = 0;
let d1 = 0;
let d2 = 0;
let time = 0;
//定数
const xo = 200;
const yo = 400;
const dt = 0.01;
const G = 0.13;
let setgraf = () =>{
//グラフの軸
cn.beginPath();
cn.moveTo(xo,yo);
cn.lineTo(xo+300,yo);
cn.stroke();
cn.beginPath();
cn.moveTo(xo,yo);
cn.lineTo(xo,yo-300);
cn.stroke();
cn.beginPath();
cn.moveTo(xo,yo);
cn.lineTo(xo-150,yo+150);
cn.stroke();
//目盛り
for (i = 0; i < 11; i++) {
cn.beginPath();
cn.moveTo(xo,yo-i*30);
cn.lineTo(xo-5,yo-i*30);
cn.stroke();
cn.beginPath();
cn.moveTo(xo,yo-i*30);
cn.lineTo(xo-5,yo-i*30);
cn.stroke();
cn.beginPath();
cn.moveTo(xo+i*30,yo);
cn.lineTo(xo+i*30,yo+5);
cn.stroke();
cn.beginPath();
cn.moveTo(xo-i*15,yo+15*i);
cn.lineTo(xo-i*15-3,yo+15*i-2);
cn.stroke();
cn.font = "10px 'Alial'";
if (0 < i) {
cn.fillStyle = "rgb(0,0,0)";
cn.fillText(i-5,xo+30*i,yo+15);
cn.fillText(i-5,xo-25,yo-30*i);
cn.fillText(i-5,xo-15*i-15,yo+15*i);
}
};
cn.font = "20px 'Alial'";
cn.fillText("x",xo-160,yo+170);
cn.fillText("y",xo+310,yo);
cn.fillText("z",xo,yo-310);
//点線
cn.save();
cn.setLineDash([2, 8]);
cn.beginPath();
cn.moveTo(xo+300,yo);
cn.lineTo(xo+300,yo-300);
cn.lineTo(xo,yo-300);
cn.lineTo(xo-150,yo-150);
cn.lineTo(xo-150,yo+150);
cn.lineTo(xo,yo+150);
cn.lineTo(xo+150,yo+150);
cn.lineTo(xo+150,yo-150);
cn.lineTo(xo-150,yo-150);
cn.stroke();
cn.beginPath();
cn.moveTo(xo+150,yo-150);
cn.lineTo(xo+300,yo-300);
cn.stroke();
cn.beginPath();
cn.moveTo(xo+150,yo+150);
cn.lineTo(xo+300,yo);
cn.stroke();
cn.restore();
//太陽
cn.beginPath();
cn.arc(xo+75,yo-75,4,0,Math.PI*2);
cn.stroke();
};
setgraf()
//10ミリ秒毎にcanvasを描写
let setI = setInterval(()=>{
//時間(月)
cn.clearRect(10,10,200,50);
cn.fillText(Math.round(time)+"month",50,30);
console.log(time)
//惑星1
cn.beginPath();
cn.arc(
xo+75-15*x1+30*y1,yo-75+15*x1-30*z1,
0.5,0,Math.PI*2);
cn.fillStyle = "rgb(250,150,150)"
cn.fill();
//惑星2
cn.beginPath();
cn.arc(
xo+75-15*x2+30*y2,yo-75+15*x2-30*z2,
0.5,0,Math.PI*2);
cn.fillStyle = "rgb(150,150,255)";
cn.fill();
// 次の描写時の位置を決めるための計算
d12 = ((x1-x2)**2+(y1-y2)**2+(z1-z2)**2)**(3/2);
d1 = ((x1)**2+(y1)**2+(z1)**2)**(3/2);
d2 = ((x2)**2+(y2)**2+(z2)**2)**(3/2);
vx1 = vx1 - G*(mas0*x1/d1+mas2*(x1-x2)/d12)*dt;
vy1 = vy1 - G*(mas0*y1/d1+mas2*(y1-y2)/d12)*dt;
vz1 = vz1 - G*(mas0*z1/d1+mas2*(z1-z2)/d12)*dt;
x1 = x1 + vx1*dt;
y1 = y1 + vy1*dt;
z1 = z1 + vz1*dt;
vx2 = vx2 - G*(mas0*x2/d2+mas1*(x2-x1)/d12)*dt;
vy2 = vy2 - G*(mas0*y2/d2+mas1*(y2-y1)/d12)*dt;
vz2 = vz2 - G*(mas0*z2/d2+mas1*(z2-z1)/d12)*dt;
x2 = x2 + vx2*dt;
y2 = y2 + vy2*dt;
z2 = z2 + vz2*dt;
time = time +dt;
},10);
// ボタンを押すとinputの値を再取得する仕組み
but1.addEventListener("click",()=>{
inputs = document.getElementsByTagName("input");
time = 0;
mas0 = 1*inputs[0].value;
mas1 = 1*inputs[1].value;
x1 = 1*inputs[2].value;
y1 = 1*inputs[3].value;
z1 = 1*inputs[4].value;
vx1 = 1*inputs[5].value;
vy1 = 1*inputs[6].value;
vz1 = 1*inputs[7].value;
mas2 = 1*inputs[8].value;
x2 = 1*inputs[9].value;
y2 = 1*inputs[10].value;
z2 = 1*inputs[11].value;
vx2 = 1*inputs[12].value;
vy2 = 1*inputs[13].value;
vz2 = 1*inputs[14].value;
cn.clearRect(0,0,width,height);
setgraf();
});
</script>

