(i)　電子が飛び出ない場合 \[h\nu\le W\] 仕事関数\(W\)以上のエネルギーを光子からもらっていないため電子は飛び出さない。

(ii)　電子が飛び出る場合 \[h\nu-W=K_e\] 光子のエネルギー\(h\nu\)と仕事関数\(W\)の差が電子の運動エネルギー\(K_e\)となる。

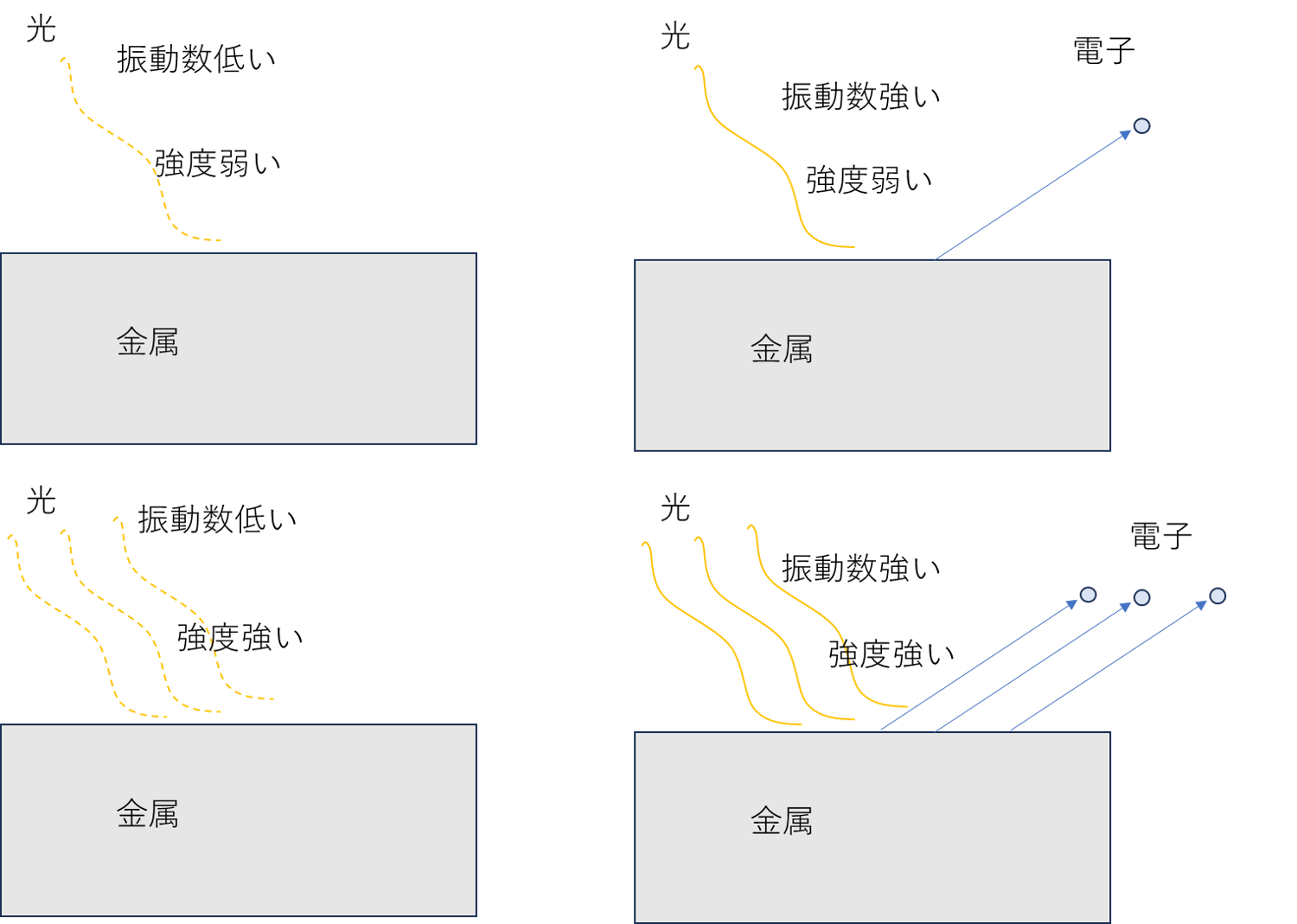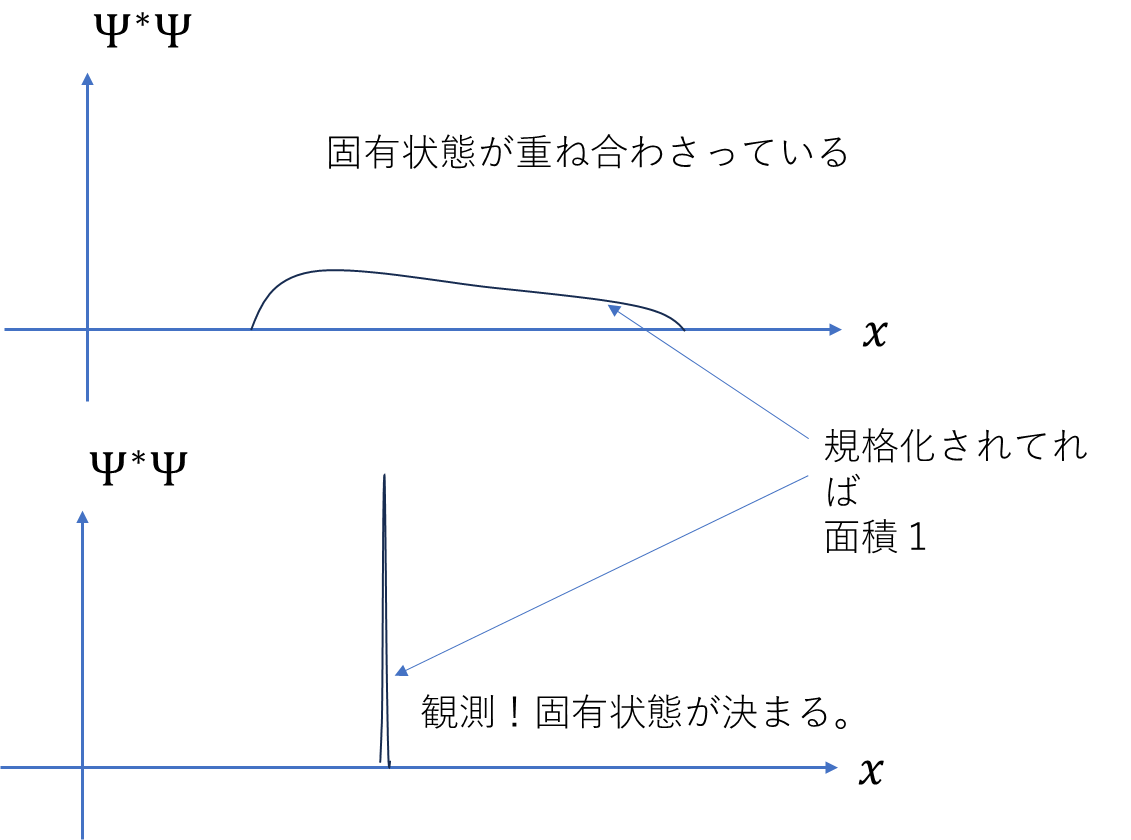
波動関数は観測により１つに決まるが、まったく同じ状況を作っても波動関数が収縮する場所は違う。\(\Psi^*\Psi\)が確率に比例しているので、\(\Psi^*\Psi\)が大きい所だとそこに収縮しやすい。逆に\(\Psi^*\Psi=0\)の場所には収縮しない。＊＊/

/＊＊簡単にまとめた物理量のルール　簡単にするため１次元

(i)　物理量演算子\(\hat{A}\)左からを固有状態の波動関数\(\psi_n\)に作用させて固有値\(A_n\)を求める。 \[\hat{A}\psi_n=A_n\psi_n\] 観測するごとに固有関数\(\psi_n\)が異なるので、固有値\(A_n\)も毎回異なる。 位置演算子\(\hat{x}\)は扱いが特別で、 \[\hat{x}\psi_n=x\psi_n\] 固有関数\(\psi\)による固有値を与えてくれないだた一の変数\(x\)を掛けるだけである。

(ii)　位置\(x\)、運動量\(p\)を量子化すると、 \[\hat{x}:=x\] \[\hat{p}:=\frac{\hbar}{i}\frac{\partial}{\partial x}\] となる。\(\hbar=h/(2\pi)\)はディラック定数これは定義でありこれ以上の説明はない。

(iii)　固有関数\(\psi_n\)が決まらなくても波動関数\(\Psi\)から物理量\(A\)の期待値\(\langle A\rangle\)は求められる。 \[\langle A\rangle=\int_{-\infty}^{\infty}\Psi^*\hat{A}\Psi dx\] なぜかこの積分で期待値が求められる。

運動量演算子\(\hat{p}\)が \[\hat{p}:=\frac{\hbar}{i}\frac{\partial}{\partial x}\] と定義されたことが役に立つ。２つの状態１と２の固有関数\(\psi_1,\psi_2\)について、 \[\int_{-\infty}^{\infty}(\hat{p}\psi_1)^*\psi_2dx=\int_{-\infty}^{\infty}\left(\frac{\hbar}{i}\frac{\partial\psi_1}{\partial x}\right)^*\psi_2dx=\int_{-\infty}^{\infty}-\frac{\hbar}{i}\frac{\partial\psi_1^*}{\partial x}\psi_2dx\] ここで置換積分を使って \[=\left[-\frac{\hbar}{i}\psi_1^*\psi_2\right]_{-\infty}^{\ \infty}+\int_{-\infty}^{\infty}\psi_1^*\frac{\hbar}{i}\frac{\partial\psi_2}{\partial x}dx\] \(\psi_n^*\psi_n\)は物質の存在確率密度で無限遠では０であると考えられるので、\(\psi_n(\pm\infty)=0\)なので１項目は０になり、 \[\int_{-\infty}^{\infty}(\hat{p}\psi_1)^*\psi_2dx=\int_{-\infty}^{\infty}\psi_1^*\hat{p}\psi_2dx\] \(\hat{p}\)の状態1の固有値を\(p_1\)、状態1の固有値を\(p_2\)とすると、 \[p_1^*\int_{-\infty}^{\infty}\psi_1^*\psi_2dx=p_2\int_{-\infty}^{\infty}\psi_1^*\psi_2dx\] \(p_1^*,p_2\)は定数なので積分の外に出した。運動量は実数なので複素共役を取っても変わらないので、全部左辺にまとめて \[(p_1-p_2)\int_{-\infty}^{\infty}\psi_1^*\psi_2dx=0\] \(p_1-p_2\)で両辺を割る。 \[\int_{-\infty}^{\infty}\psi_1^*\psi_2dx=0\] 以上より \[\int_{-\infty}^{\infty}\psi_m^*\psi_ndx=\begin{cases}0&(m\neq n)\\1&(m=n)\end{cases}\] 同じ固有関数同士であれば規格化条件から積分の値は１になる。これは運動量演算子から求まった性質だが一般的に成り立つものとする。なんだか単位ベクトルの内積に似ているため直交性と呼ばれたりする。あとは簡単。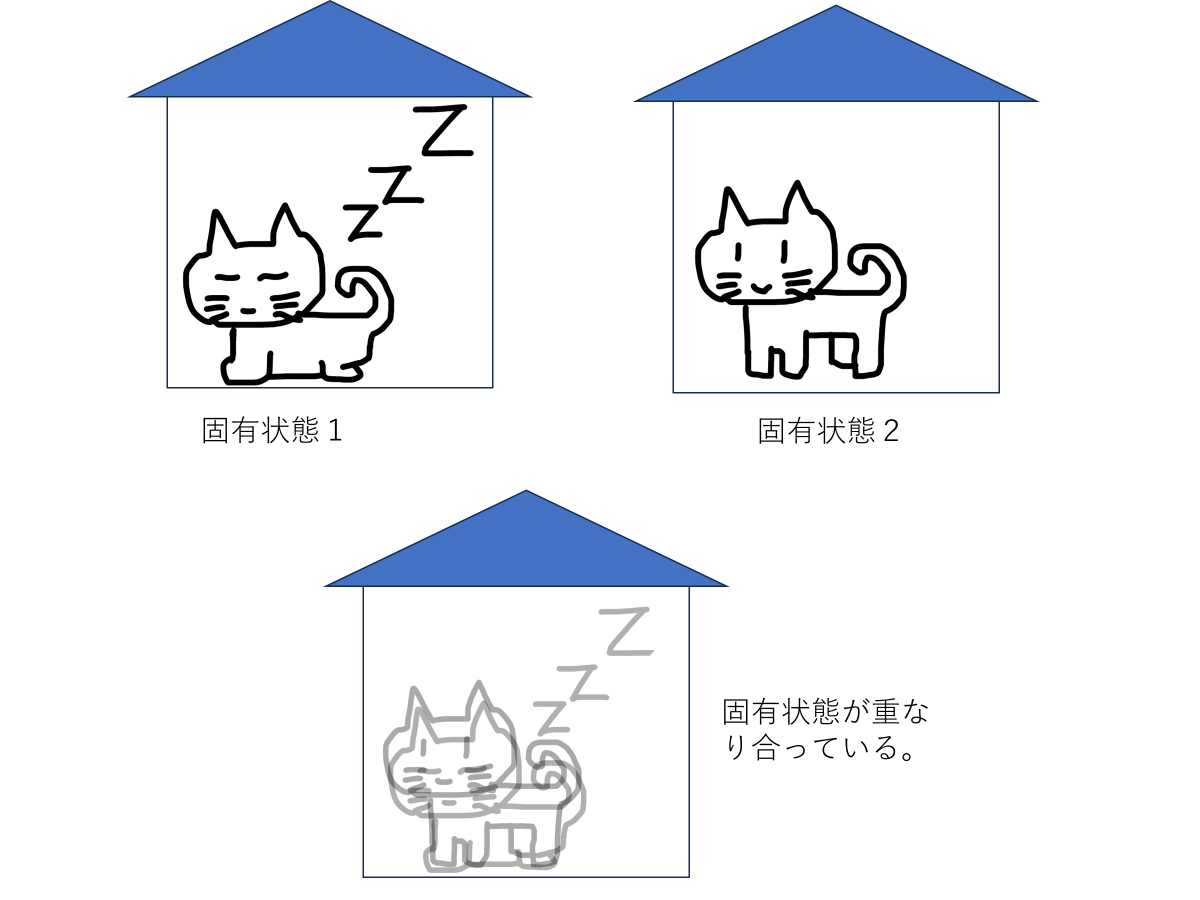演算子\(\hat{A}\)を波動関数\(\Psi\)の左側に作用させると、 \[\Psi=c_1\psi_1+c_2\psi_2+\cdots+c_n\psi_n\] \[\hat{A}\Psi=\hat{A}(c_1\psi_1+c_2\psi_2+\cdots+c_n\psi_n)\] \[=c_1A_1\psi_1+c_2A_2\psi_2+\cdots+c_nA_n\psi_n\] \(\Psi^*\)を掛ける。 \[\Psi^*\hat{A}\Psi=c_1^2A_1\psi_1\psi_1^*+c_2^2A_2\psi_2\psi_2^*+\cdots+c_n^2A_n\psi_n\psi_n^*\] \[+\sum_{\mu\neq\nu}c_\mu c_\nu A_\nu\psi_\mu^*\psi_\nu\] 両辺を定義域で積分すると、添え字が同じなら\(\int\psi_m\psi_m dx=1\)それ以外0になるので、 \[\int_{-\infty}^{\infty}\Psi^*\hat{A}\Psi dx=c_1^2A_1+c_2^2A_2+\cdots+c_n^2A_n=\langle A \rangle\tag{3}\] これが得たかった式である。\(\hat{A}=1\)とすると \[c_1^2+c_2^2+\cdots+c_n^2=\int_{-\infty}^{\infty}\Psi^*\Psi dx=1\] \(c_n^2\)の総和が１になることから、\(c_n^2\)は固有状態\(n\)が実現する確率と解釈すれば(3)式が期待値となる。特別な演算子\(\hat{x}\)について、\(\Psi(x)^*\Psi(x)\)がそもそも粒子の存在確率の密度なので、\(x\)の関数\(f(x)\)についても(3)式で期待値が計算できる。 \[\int_{-\infty}^{\infty}x\Psi^*\Psi dx=\int_{-\infty}^{\infty}x\times確率密度 dx=\langle x\rangle\] \[\int_{-\infty}^{\infty}f\Psi^*\Psi dx=\int_{-\infty}^{\infty}f\times確率密度dx=\langle f\rangle\]

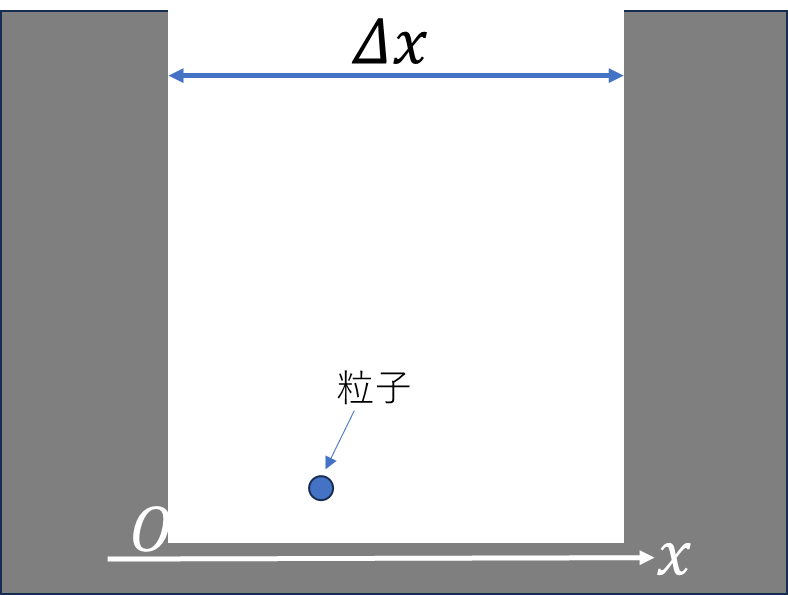
　よく無限に深い井戸型ポテンシャルと呼ばれる状況にいる粒子について考えてみる。粒子のポテンシャルエネルギー\(U\)は、 \[U(x)=\begin{cases}\infty&(x\le0) \\0&(0\lt x\lt\varDelta x) \\\infty&(\varDelta x\le x)\end{cases}\] 力学的エネルギー\(E\)の量子化を考える。記号を\(\hat{H}\)として、 \[\hat{H}:=\frac{\hat{p}^2}{2m}+U(\hat{x})\] \[=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+U\] で定義しよう。\(\hat{x}=x\)なのでそのように書いても同じことである。演算子\(\hat{H}\)を固有関数\(\psi_n\)が分かっていれば左から作用させ、 \[\hat{H}\psi_n=\frac{\hat{p}^2}{2m}\psi_n+U(x)\psi_n\] \[=\left(\frac{p^2_n}{2m}+U(x)\right)\psi_n=E_n\psi_n\tag{4}\] とエネルギーの固有値\(E_n\)が求まるものとする。井戸型ポテンシャルの条件から(4)式を解いて、固有関数\(\psi\)を求めてみよう。\(0\lt x\lt\varDelta x\)の範囲で \[-\frac{\hbar^2}{2m}\frac{\partial^2\psi}{\partial x^2}=E\psi\] \[\frac{\partial^2\psi}{\partial x^2}=-\frac{2mE}{\hbar^2}\psi\] これは単振動と同じ形の方程式だから、 \[\psi=C\sin\frac{\sqrt{2mE}}{\hbar}x\] オイラーの公式\(\sin\alpha=(e^{i\alpha}-e^{-i\alpha})/2i\)を使って、 \[\psi=C\frac{\exp(i\sqrt{2mE}x/\hbar)-\exp(-i\sqrt{2mE}x/\hbar)}{2i}\] 実はこの関数固有関数\(\psi\)になっていない。 \[\psi_+=C\frac{\exp(i\sqrt{2mE}x/\hbar)}{2i}\] \[\psi_-=-C\frac{\exp(-i\sqrt{2mE}x/\hbar)}{2i}\] の２つの固有関数の重ね合わせになっている。運動量演算子を作用させると、 \[\hat{p}\psi_{+}=\frac{\hbar}{i}\frac{\partial\psi_+}{\partial x}=+\sqrt{2mE}\psi_+\] \[\hat{p}\psi_{-}=\frac{\hbar}{i}\frac{\partial\psi_-}{\partial x}=-\sqrt{2mE}\psi_-\] 運動量固有値は、固有関数\(\psi_\pm\)の固有値は\(p=\pm\sqrt{2mE}\)となる。 固有関数\(\psi_\pm\)にハミルトニアン演算子\(\hat{H}\)を作用させると、(結果が同じなので同時にやる。) \[\hat{H}\psi_\pm=-\frac{\hbar^2}{2m}\frac{\partial^2\psi_\pm}{\partial x^2}\] \[=-\frac{\hbar^2}{2m}\left(\pm\frac{i\sqrt{2mE}}{\hbar}\right)\left(\pm\frac{i\sqrt{2mE}}{\hbar}\right)\psi_\pm=E\psi_\pm\] どちらの固有関数でもエネルギー固有値は\(E\)となる。ちょっと屁理屈っぽい解釈だが、これを次のように解釈する。

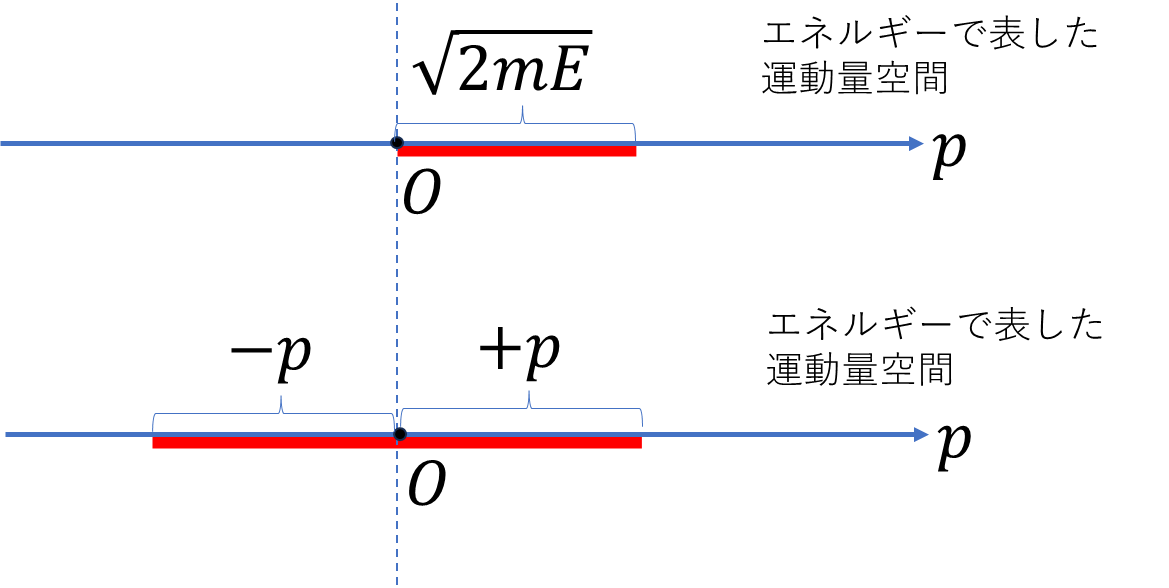
エネルギーを使った運動量空間(直線)で粒子のエネルギーの体積(線分の長さ)は運動量表示の運動量空間の半分の体積であると考えることにしよう。エネルギーは常に\(E\gt0\)だが粒子がどっち向きに運動しているか分からないためである。 粒子が壁の内側にいるので、\(\psi(x=0)=\psi(x=\varDelta x)=0\)でなくてはならない。 \[\psi=C\sin\frac{\sqrt{2mE}}{\hbar}\varDelta x=0\] これを満たすには、 \[\frac{\sqrt{2mE}}{\hbar}\varDelta x=n\pi\ (n=1,2,\cdots)\] 粒子は運動しているので、\(E\gt0\)そのため\(n=0\)は除かれる。\(n\)は１以上となる。\(\hbar=h/(2\pi)\)だから、 \[\sqrt{2mE}=\frac{h}{2\varDelta x}n\] なので、\(\sqrt{2mE}\)は\(h/(2\varDelta x)\)の整数倍の飛び飛びの値を取る。

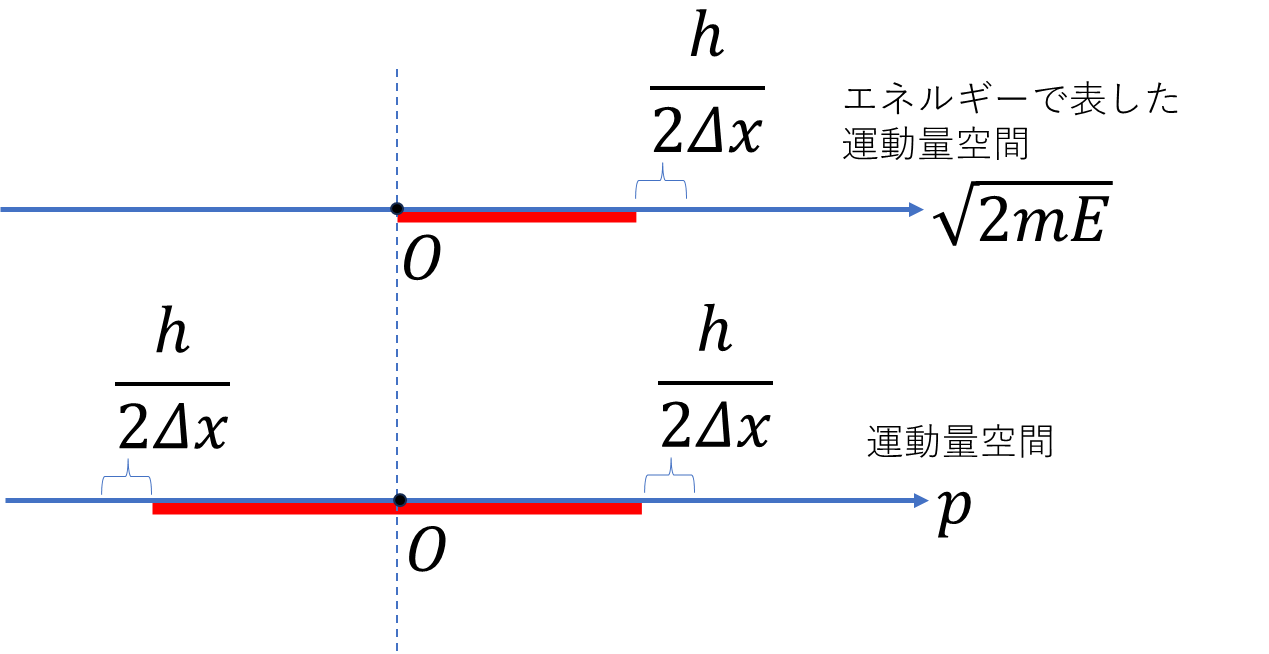
エネルギーが\(h/2\)変化するときによる運動量\(p\)の変化は \[\varDelta p=\frac{h}{\varDelta x}\] これは最小の運動量の変化量なので一般に \[\varDelta p\ge\frac{h}{\varDelta x}\] \[\varDelta x\varDelta p\ge h\] が成り立つ。

今から少し準備をする。\(u(\pm\infty)=v(\pm\infty)=0\)となる複素数値関数\(u(x),v(x)\)について、 \[\int_{-\infty}^{\infty}(\hat{A}u)^*vdx=\int_{-\infty}^{\infty}u^*\hat{A}vdx\] となる演算子\(\hat{A}\)をエルミート演算子という。運動量演算子\(\hat{p}\)はエルミート演算子である。固有関数の直交性の証明と同じことをやると、 \[\int_{-\infty}^{\infty}(\hat{p}u)^*vdx=\int_{-\infty}^{\infty}\left(\frac{\hbar}{i}\frac{\partial u}{\partial x}\right)^*vdx=\int_{-\infty}^{\infty}-\frac{\hbar}{i}\frac{\partial u^*}{\partial x}vdx\] \[=\left[-\frac{h}{i}u^*v\right]_{-\infty}^{\ \infty}-\int_{-\infty}^{\infty}-\frac{\hbar}{i}\frac{\partial v}{\partial x}u^*dx=\int_{-\infty}^{\infty}u^*\hat{p}vdx\] 実数関数を掛ける操作\(f(x)\times\)も演算子とみなせばエルミートである。 \[\int_{-\infty}^{\infty}(fu)^*vdx=\int_{-\infty}^{\infty}fu^*vdx=\int_{-\infty}^{\infty}u^*fvdx\] 一般に実数関数で示したが使うのは位置\(f=x\)と定数関数\(f=C\)だけ。次にエルミート演算子の和もエルミート演算子であることを示す。エルミート演算子\(\hat{A},\hat{B}\)について、 \[\int_{-\infty}^{\infty}\{(\hat{A}+\hat{B})u\}^*vdx=\int_{-\infty}^{\infty}\{(\hat{A}u)^*+(\hat{B}u)^*\}vdx\] \[=\int_{-\infty}^{\infty}(\hat{A}u)^*vdx+\int_{-\infty}^{\infty}(\hat{B}u)^*vdx\] \[=\int_{-\infty}^{\infty}u^*\hat{A}vdx+\int_{-\infty}^{\infty}u^*\hat{B}vdx=\int_{-\infty}^{\infty}u^*(\hat{A}+\hat{B})vdx\] 演算子\(\hat{A},\hat{B}\)を \[\hat{A}=\hat{x}-\langle x\rangle\] \[\hat{B}=\hat{p}-\langle p\rangle\] とする。\(\langle x\rangle,\langle p\rangle\)は、それぞれ\(x,p\)の期待値で定数であるため、エルミートである。交換子\([x,y]:=xy-yx\)を定義して、 \[[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A}\] \[=(\hat{x}-\langle x\rangle)(\hat{p}-\langle p\rangle)-(\hat{p}-\langle p\rangle)(\hat{x}-\langle x\rangle)\] \[=(\hat{x}\hat{p}-\hat{x}\langle p\rangle-\langle x\rangle\hat{p}+\langle x\rangle\langle p\rangle)\] \[-(\hat{p}\hat{x}-\langle x\rangle\hat{p}-\hat{x}\langle p\rangle+\langle x\rangle\langle p\rangle)=[\hat{x},\hat{p}]\] \([\hat{A},\hat{B}]=[\hat{x},\hat{p}]\)とわかった。 \[[\hat{x},\hat{p}]\Psi=x\frac{\hbar}{i}\frac{\partial \Psi}{\partial x}-\frac{\hbar}{i}\frac{\partial}{\partial x}x\Psi\] \[=x\frac{\hbar}{i}\frac{\partial \Psi}{\partial x}-\frac{\hbar}{i}\Psi-x\frac{\hbar}{i}\frac{\partial \Psi}{\partial x}\] \[[\hat{x},\hat{p}]\Psi=i\hbar\Psi\] 位置演算子と運動量演算子の交換子が\(i\hbar\)になるというきれいな関係が得られた。これで準備OK。次の積分を計算する。ただし\(\alpha\in\mathbb{R}\) \[\int_{-\infty}^{\infty}\{(\hat{A}\alpha+i\hat{B})\Psi\}^*\{(\hat{A}\alpha+i\hat{B})\Psi\}dx\ge0\] 被積分関数は複素共役の積なので０以上となる。(すいませんが、積分記号を省略させてください) \[\{(\hat{A}\alpha+i\hat{B})\Psi\}^*\{(\hat{A}\alpha+i\hat{B})\Psi\}\] \[=\{(\hat{A}\Psi)^*\alpha-i(\hat{B}\Psi)^*\}(\hat{A}\Psi\alpha+i\hat{B}\Psi)\] \[=\{(\hat{A}\Psi)^*\alpha-i(\hat{B}\Psi)^*\}\hat{A}\Psi\alpha+i\{(\hat{A}\Psi)^*\alpha-i(\hat{B}\Psi)^*\}\hat{B}\Psi\] \[=(\hat{A}\Psi)^*\hat{A}\Psi\alpha^2+i\{(\hat{A}\Psi)^*\hat{B}\Psi-(\hat{B}\Psi)^*\hat{A}\Psi\}\alpha+(\hat{B}\Psi)^*\hat{B}\Psi\] エルミート演算子の性質を使って演算子を全て共役じゃない波動関数\(\Psi\)の方に持ってくると、 \[=\Psi^*\hat{A}^2\Psi\alpha^2+\Psi^*i[\hat{A},\hat{B}]\Psi\alpha+\Psi^*\hat{B}^2\Psi\] \([x,y]:=xy-yx\)で定義される交換子と呼ばれるものだ。3つの項が出てきたがまずは１項目から、\(\alpha^2\)を除いて、 \[\int_{-\infty}^{\infty}\Psi^*\hat{A}^2\Psi dx=\int_{-\infty}^{\infty}\Psi^*(x-\langle x\rangle)^2\Psi dx\] \[=\int_{-\infty}^{\infty}\Psi^*x^2\Psi dx-2\langle x\rangle\int_{-\infty}^{\infty}\Psi^*x\Psi dx+\langle x\rangle^2\int_{-\infty}^{\infty}\Psi^*\Psi dx\] \[=\langle x^2\rangle-2\langle x\rangle\langle x\rangle+\langle x\rangle^2=\langle x^2\rangle-\langle x\rangle^2=\sigma_x^2\] ２乗平均と平均の差なので分散\(\sigma_x^2\)になる。第３項目もほぼ同じ計算で、\(\sigma_p^2\)となる。\(\alpha\)を除く第２項目は \[\int_{-\infty}^{\infty}\Psi^*i[\hat{A},\hat{B}]\Psi dx=\int_{-\infty}^{\infty}\Psi^*i[\hat{x},\hat{p}]\Psi dx\] \[=i^2\hbar\int_{-\infty}^{\infty}\Psi^*\Psi dx=-\hbar\] 以上から、 \[\int_{-\infty}^{\infty}\{(\hat{A}\alpha+i\hat{B})\Psi\}^*\{(\hat{A}\alpha+i\hat{B})\Psi\}dx\ge0\] \[\sigma_x^2\alpha^2-\hbar\alpha+\sigma_p^2\ge0\] \[\sigma_x^2\left(\alpha-\frac{\hbar}{2\sigma_x^2}\right)^2-\frac{\hbar^2}{4\sigma_x^2}+\sigma_p^2\ge0\] 任意の\(\alpha\)で１項目は０以上だから、 \[-\frac{\hbar^2}{4\sigma_x^2}+\sigma_p^2\ge0\] \[\sigma_x\sigma_p\ge\frac{\hbar}{2}\] となる。