直線上の運動のでも本質を損なうことがないので、簡単のため1次元の話をする。ニュートン力学では時間\(t\)や物の長さ\(l\)は誰から見ても同じものであった。ニュートン力学でやったガリレイ変換というものを覚えているだろうか。座標\(K,\ K'\)があり時刻\(t=0\)で、原点は一致している。\(K\)は静止して、\(K'\)は一定の速度\(V\)で動く。ある物体が運動しているとしよう。座標系\(K\)でその物体の運動方程式が \[F(x,t)=m\frac{d^2x(x,t)}{dt^2}\] である。\(K\)からみて速度\(V\)で進んでいる座標系\(K'\)では、物体の運動方程式が \[F'(x,t)=m\frac{d^2x'(x,t)}{dt^2}\] となったとする。物体の位置は図より\(x'=x-Vt\)であるから \[F'=m\frac{d}{dt}\left(\frac{d(x-Vt)}{dt}\right)=m\frac{d}{dt}\left(\frac{dx}{dt}-V\right)=m\frac{d^2x}{dt^2}=F\] つまり\(x\mapsto x-Vt,v\mapsto v-V\)のような変換に対して運動方程式は不変である。これがガリレイ変換不変性。もっと簡単な言葉でいえば等速直線運しているしている系ならどの系から見ても物体の運動方程式は等しい。単振動を例に挙げると、自然長の位置\(x_0\)と物体の位置\(x\)とすると、 \[F=-k(x-x_0)\] \(x\mapsto x-Vt,x_0\mapsto x_0-Vt\)の変換で(ばね係数はばね固有のもの) \[F'=-k(x'-x_0')\] \[=-k((x-Vt)-(x_0-Vt))=-k(x-x_0)=F\] しかし、電荷\(q\)にはたらくローレンツ力はどうだろうか、 \[F_m=qvB\sin\theta\] この式をガリレイ変換すると、 \[F_m=q(v-V)B\sin\theta\] である。大げさに言うと電荷と並走している(同じ速度の座標系)では、\(F_m=0\)となってしまう。となりガリレイ変換が成り立たなかった。見る座標系により電荷にはたらく力が違って見えてしまう。この問題の解決は今後やる予定なのでお楽しみを。

　まずは特殊相対性理論を構成する２つの原理を紹介しよう。

＊＊光速度不変の原理＊＊

　光の速さは光源の運動状態によらず、だれから見ても\(c:=299\ 792\ 458 \mathrm{m\ s^{-1}}\)である。

＊＊特殊相対性原理＊＊

　物理法則はどの慣性系から見ても同じ形で表せる。(同じ形だが時間や距離はその慣性系固有のものである。)

　この２つの原理を出発点として各慣性系の距離、時間、物理法則を再定義することになる。どこまで覆して再出発しなければいけないか見てみよう。

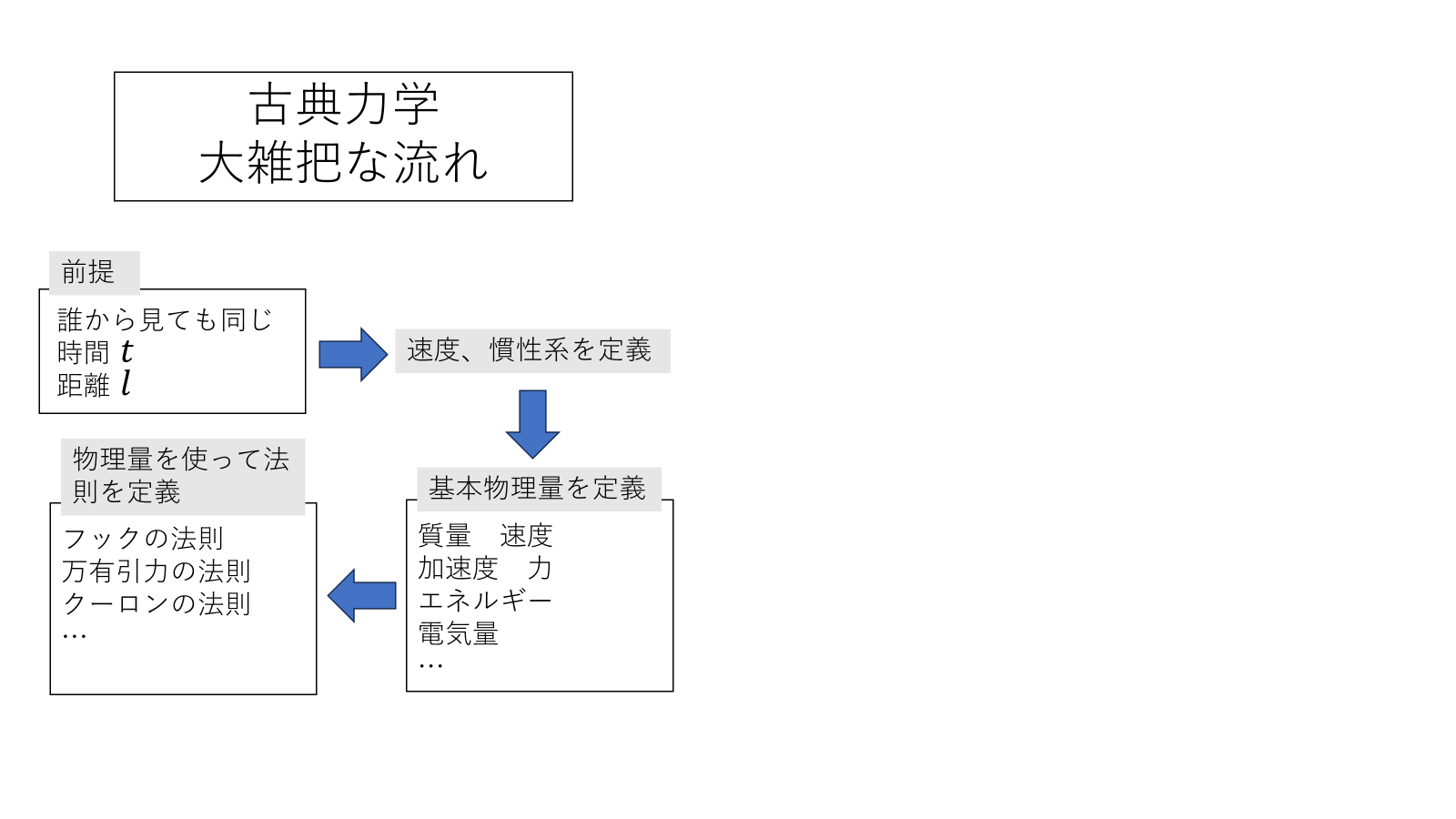
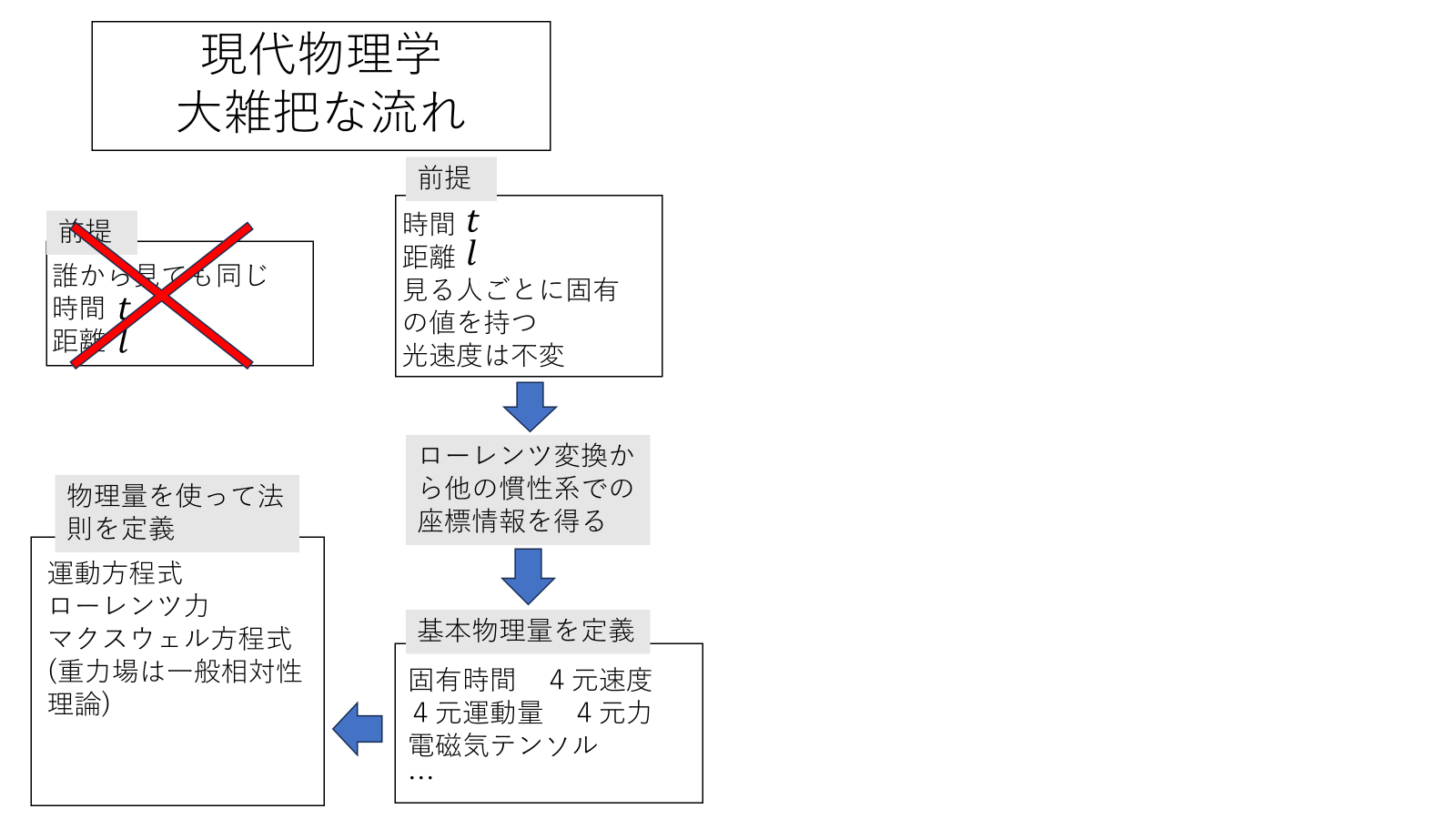
　ようは光速は誰から見ても同じなので速度\(v\)で光を追いかけても光の速さは\(c-v\)とはならず追いかけてる人から見ても\(c\)である。またこっちで測って\(l\)だったからあっちから見ても長さが\(l\)とか、自分から見て時刻\(t\)で物体が衝突したから、向こうから見ても時刻\(t\)でぶつかっているはずなど、当たり前であった感覚が先入観になる。慣性系同士で物理法則の形が変わらない、光の速さは誰から見ても変わらないほうにつじつまを合わせたら、時間、空間が慣性系固有のものになってしまったのだ。

　ここが特殊相対性理論で1番難しい所だと思う。素直にローレンツ変換を受け入れるのは無理だと思う。しかし運動方程式が特殊相対性原理を満たすように補正を入れると、電磁気の方程式はローレンツ変換不変性を満たすので直観に反するようで、ローレンツ変換が正しいことが実感できるはずである。

　使いまわしであるが、この図を使ってローレンツ変換を説明しよう。"これは\(K\)からみた図"である。\(K'\)から見ると\(K\)が\(V'\)で遠ざかっている。相互作用がない真空中で物体が等速直線運動する系を慣性系とする。座標系\(K,\ K'\)がありそれぞれの時刻\(t=t'=0\)の時にそれぞれの原点\(O,O'\)が一致していたとしよう。\(K\)から見ると\(K'\)は一定の速度\(V\)で進んでいる。物体の位置は\(K\)から見ると時刻\(t\)に\(x\)にある。\(K'\)から見ると時刻\(t'\)には\(x'\)にある。\(K\)から見たと\(x',t'\)は \[\begin{pmatrix}ct'(ct,x)\\x'(ct,x)\end{pmatrix}=\begin{pmatrix}a_{11}ct(ct',x')+a_{12}x(ct',x')\\a_{21}ct(ct',x')+a_{22}x(ct',x')\end{pmatrix}\tag{1}\] \[\begin{pmatrix}ct'(ct,x)\\x'(ct,x)\end{pmatrix}=A(V)\begin{pmatrix}ct(ct',x')\\x(ct',x')\end{pmatrix}\] (時空間で時間を距離と同等に扱うので、時間と距離で単位が違うと違和感があるので光速度を掛けておきます。なくても大丈夫です。) \(K'\)からみた\(x,t\)は\(K'\)から見れば\(K\)は速度\(-V\)で進んでいる。(速度\(V\)で下がっている。)ので \[\begin{pmatrix}ct(ct',x')\\x(ct',x')\end{pmatrix}=A(-V)\begin{pmatrix}ct'(ct,x)\\x'(ct,x)\end{pmatrix}\] のような１次変換が成り立っていてほしい。なぜ１次変換かというと、ルートとか２乗とかが\(x,t\)にかかると変換と逆変換の形がちがうものになってしまうからである。\(K,\ K'\)の間で違うのは速度\(V\)が逆向きなだけなので、 \[A(V)^{-1}=A(-V)\] ローレンツ変換の\(V\)の符号を逆にしたら逆変換になってほしい。抽象的過ぎた。概要はここまで、実際にローレンツ変換を求めていこう。\(K\)の\(O\)から見て、\(K'\)の\(O'\ (x'=0)\)の位置は\(x(ct',0)=Vt\)に見えるので、(1)式下の 段を使い \[x'=a_{21}ct+a_{22}x\] \[0=a_{21}ct+a_{22}Vt,\ a_{21}=-\frac{V}{c}a_{22}\] \(V/c=\beta\)とすると \[x'=a_{22}(-\beta ct+x)\tag{2}\] ここで、\(x\)軸、\(x'\)軸を負の方向に取ると、物体の位置は、\(K,K'\)でそれぞれ\(-x,-x'\)更に\(K'\)から見て\(K\)は\(-x'\)軸方向に速度\(V\)で進むため、(2)と同じ変換が使えるはずである。 \[-x=a_{22}(-\beta ct'-x')\] \[x=a_{22}(\beta ct'+x')\tag{3}\] (2)式、(3)式から\(x'\)を消去 \[x=a_{22}(\beta ct'-a_{22}\beta ct+a_{22}x)\] \[-\beta ct'=\left(a_{22}-\frac{1}{a_{22}}\right)x-a_{22}\beta ct\] \[ct'=a_{22} ct+\frac{1-a_{22}^2}{\beta a_{22}}x\tag{4}\] これで\(a_{11},a_{12}\)も\(a_{22}\)がわかれば求まる。個光速度不変の原理より、光の速さは誰から見ても変わらないので、時刻\(t=t'=0\)、原点\(O\)で発した光の位置は\(x=ct,\ x'=ct'\)で表せる。(4)式、(2)式から\(x',t'\)を消去。 \[x'=ct'=a_{22} ct+\frac{1-a_{22}^2}{\beta a_{22}}x\] \[a_{22}(-\beta ct+x)=a_{22} ct+\frac{1-a_{22}^2}{\beta a_{22}}x\] \(x=ct\)を代入。 \[a_{22}(-\beta ct+ct)=a_{22} ct+\frac{1-a_{22}^2}{\beta a_{22}}ct\] \[-\beta ^2a_{22}^2+\beta a_{22}^2=\beta a_{22}^2+1-a_{22}^2\] \[a_{22}^2=\frac{1}{1-\beta^2},\ a_{22}=\frac{1}{\sqrt{1-\beta^2}}\] \(1/\sqrt{1-\beta^2}=\gamma\)する。これを(2)(4)に代入すると、 \[ct'=\gamma ct-\beta\gamma x\] \[x'=-\beta\gamma ct+\gamma x\tag{5}\] 相対性理論では、テンソルを使うことが多いので今のうちから慣れておこう。ベクトルは\(\boldsymbol{x}\)ではなく\(x^{\mu}\)のようにかく。 \[x^{0}=ct,\ x^{1}=x\] のように添え字(右上の小さい文字１つ)で成分が１つ決まるものをベクトルという。基底ベクトルを書かなくていいのでシンプルだが累乗(指数)と見間違えやすいという欠点もある。 \[x^{\mu}\quad(\mu=0,1)\] と書くだけで、\(ct\)と\(x\)の両方を表していることになる。 この表記法により添え字を2つ以上決めると、成分が１つ決まるものを定義できるこれをテンソルという。 ローレンツ変換\(L^{\mu}_{\ \nu}\)は \[L^{0}_{\ 0}=\gamma\quad L^{0}_{\ 1}=-\beta\gamma\] \[L^{1}_{\ 0}=-\beta\gamma\quad L^{1}_{\ 1}=\gamma\] のように4つの成分を使うことで、ローレンツ変換は \[ct'=L^{0}_{\ 0} ct+L^{0}_{\ 1} x\] \[x'=L^{1}_{\ 0} ct+L^{1}_{\ 1} x\] となる。先ほど書き換えた\(x^{\mu}\)の表記も使ってみよう。 \[x'^0=L^{0}_{\ 0} x^0+L^{0}_{\ 1} x^1\] \[x'^1=L^{1}_{\ 0} x^0+L^{1}_{\ 1} x^1\] この表記法は\(\sum\)と相性がとてもよい。 \[x'^0=\sum_{\nu=0}^{1}L^{0\nu}x^{\nu}\] \[x'^1=\sum_{\nu=0}^{1}L^{0\nu}x^{\nu}\] 実際は\(y,z\)成分もあるので、この表記の恩恵がわかるだろう。\(x'^0,x'^1\)はベクトル\(x^{\mu}\)の成分なので、 \[x'^{\mu}=\sum_{\nu=0}^{1}L^{\mu}_{\ \nu}x^{\nu}\quad(\mu=0,1)\] このたった１つの式でローレンツ変換になる。アインシュタインの縮約記法により\(\sum\)や添え字の通し番号を省略して書くことが認められている。 \[x'^{\mu}=L^{\mu}_{\ \nu}x^{\nu}\] これは総和であることや\(\mu,\nu\)をいくつまであるのかがわかりずらいという欠点がある。ただ式はシンプルになる。こういう表記法があるよってだけで(5)式が１番大事。

＊＊ローレンツ変換＊＊

　\(K\)の時空間座標\(x^{\mu}\)と\(K\)から見て速度\(V\)で進む座標系\(K'\)の\(K\)から見た時空間座標\(x'^{\mu}\)はローレンツ変換 \[L^{0}_{\ 0}=\frac{1}{\sqrt{1-(V/c)^2}}\quad L^{0}_{\ 1}=-\frac{V/c}{\sqrt{1-(V/c)^2}}\] \[L^{1}_{\ 0}=-\frac{V/c}{\sqrt{1-(V/c)^2}}\quad L^{1}_{\ 1}=\frac{1}{\sqrt{1-(V/c)^2}}\] を使い以下のような関係になる。 \[x'^{\mu}=L^{\mu}_{\ \nu}x^{\nu}\]

　/*おまけ　ガリレイ変換は間違っているのか？　*/ \[ct'=\gamma ct-\beta\gamma x\] \[x'=-\beta\gamma ct+\gamma x\] \(\beta=V/c\)なので、 \[t'=\gamma t-\frac{V}{c^2}\gamma x\] \[x'=-\gamma Vt+\gamma x\] 速さ\(V\)が光の速さ\(c\)より十分に小さいとすると、\(V/c\simeq0\) \[\gamma=\frac{1}{\sqrt{1-(V/c)^2}}\simeq1\] なので、 \[t'=t\] \[x'=-Vt+x\] とガリレイ変換になる。日常生活で、光速度に近い系という例がほとんどないので、ガリレイ変換で十分な場合がほとんどである。