x軸上の運動で考える。ニュートン力学で運動方程式というものがあった。 \[\frac{d^2x}{dt^2}=F\] これをローレンツ変換してみたい。(運動方程式が成り立たない確認をしたいだけなので読み飛ばして大丈夫です。)まずは速度\(v\)からローレンツ変換してみよう。 \[dt'=\gamma \left(dt-\frac{V}{c^2}dx\right)\tag{1}\] \[dx'=\gamma(-Vdt+dx)\tag{2}\] (2)式÷(1)式で、 \[v'=\frac{dx'}{dt'}=\frac{dx'}{dt}\frac{dt}{dt'}=\frac{dx'}{dt}\frac{1}{\frac{dt'}{dt}}\] \[=\gamma(-V+v)\frac{1}{\gamma\left(1-\frac{V}{c^2}v\right)}\] ここから加速度\(dv'/dt'\)を求める。 \[\frac{dv'}{dt'}=\frac{dv'}{dt}\frac{1}{\frac{dt'}{dt}}\] \(dv'/dt\)は商の微分になっているのでめんどくさい。 \[=\left(\frac{1}{\left(1-\frac{V}{c^2}v\right)}\frac{dv}{dt}-(-V+v)\frac{-\frac{V}{c^2}}{\left(1-\frac{V}{c^2}v\right)^2}\frac{dv}{dt}\right)\frac{1}{\gamma\left(1-\frac{V}{c^2}v\right)}\] \[=\frac{1-\frac{V}{c^2}v-\frac{V^2}{c^2}+\frac{V}{c^2}v}{\left(1-\frac{V}{c^2}v\right)^2}\frac{1}{\gamma\left(1-\frac{V}{c^2}v\right)}\frac{dv}{dt}\] \[=\frac{1-\beta^2}{\gamma\left(1-\frac{V}{c^2}v\right)^3}\frac{dv}{dt}\] \[=\frac{1}{\gamma^3\left(1-\frac{V}{c^2}v\right)^3}\frac{dv}{dt}\] つまり別の慣性系から見ると運動方程式は、 \[\frac{m}{\gamma^3\left(1-\frac{V}{c^2}v\right)^3}\frac{dv}{dt}=F\tag{3}\] である。これはこれで事実なので、別の慣性系では運動方程式は、 \[m\frac{dv}{dt}=F\] の形で表せない。(3)式のように慣性系によって運動方程式の形が変わってしまう。

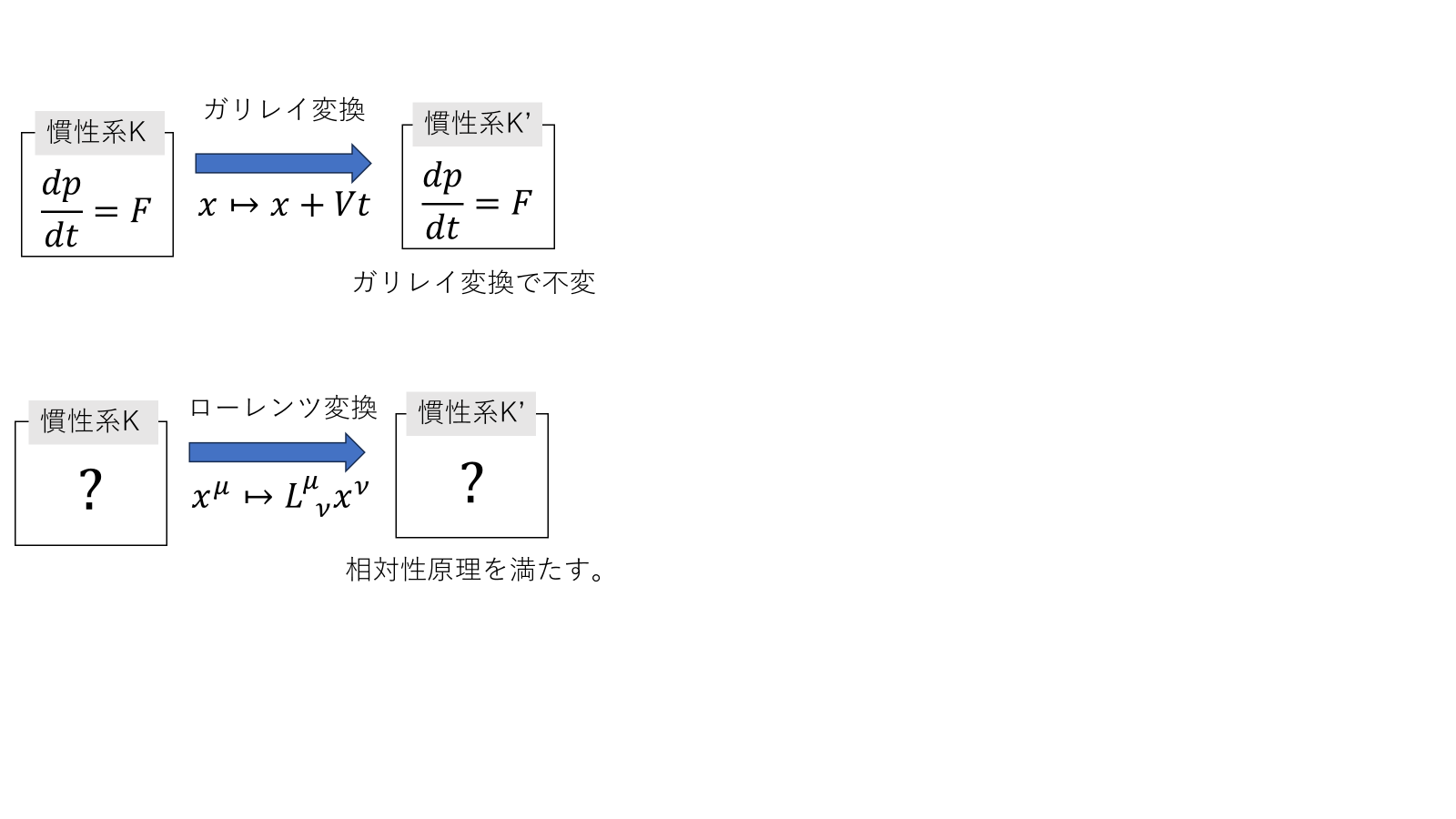
相対性原理では、どの慣性系から見ても物理法則は同じ形であらわせるという要請であり、それを満たすように物理法則を定義していく。まずは時間もベクトルになってしまったので観測者によらず同じように流れる固有時\(\tau\)を定義する。

固有時\(\tau\)を、 \[d\tau:=\frac{1}{c}\sqrt{(cdt)^2-dx^2-dy^2-dz^2}\] で定義する。加速度運動している系でも測れるよう微小量で定義してある。とても抽象的な概念なので例を出そう。\(K\)系の人が図の原点\(O\)で固有時を図ると \[\tau=\int_{0}^{t}\frac{1}{c}\sqrt{(cdt)^2-0-0-0}=\int_{0}^{t}dt\] \[\tau=t\] \(K'\)系の人から見て\(O\)の位置は\(y'=-Vt'\)なので、\(K'\)から見た\(O\)の固有時は \[\tau=\int_{0}^{t'}\frac{1}{c}\sqrt{(cdt')^2-0-(Vdt')^2-0}=\int_{0}^{t'}\sqrt{1-(V/c)^2}dt'\] \[\tau=\sqrt{1-(V/c)^2}t'\] つまり時間がゆっくり流れる系では、\(\sqrt{1-(V/c)^2}\)倍して\(\tau\)が同じになるように補正してくれる時間である。ちゃんと説明するなら、ミンコフスキー空間\(x^0,x^1,x^2,x^3\)を使うと、ルートの中身は \[(cdt)^2-dx^2-dy^2-dz^2=(dx^0)^2-(dx^1)^2-(dx^2)^2-(dx^3)^2\] 計量テンソルを使うと、 \[=-g_{\mu\nu}dx^{\mu}dx^{\nu}\] つまりミンコフスキー空間の微小距離になっている。つまりローレンツ変換に対して不変である。係数の\(1/c\)も定数なので、ローレンツ変換で不変。このことから、どこで固有時\(\tau\)を数えても同じように経過するのである。

＊＊固有時\(\tau\)＊＊

　固有時\(\tau\)を次のように定義する。 \[d\tau:=\frac{1}{c}\sqrt{-g_{\mu\nu}dx^{\mu}dx^{\nu}}\] 速度\(v\)運動している系では、 \[d\tau=\sqrt{1-(v/c)^2}dt\] である。固有時\(\tau\)はどの慣性系でも同じように経過する。

　慣性系によらない固有時が定義できたので、ミンコフスキー空間での物理量を定めていこう。まずは４元速度\(u^{\mu}\) \[u^{\mu}:=\frac{dx^{\mu}}{d\tau}\] シンプルにミンコフスキー空間の変位\(x^\mu\)を固有時\(\tau\)で微分した物理量だ。変位\(x^\mu\)のローレンツ変換は \[x'^{\mu}=L^{\mu}_{\ \nu}x^{\nu}\] なので両辺を\(\tau\)で微分して、 \[\frac{dx'^{\mu}}{d\tau}=\frac{d}{d\tau}\left(\sum_{\nu=0}^3L^{\mu}_{\ \nu}x^{\nu}\right)\] \[=\frac{d}{d\tau}(L^{\mu}_{\ 0}x^{0}+L^{\mu}_{\ 1}x^{1}+L^{\mu}_{\ 2}x^{2}+L^{\mu}_{\ 3}x^{3})\] 一応安全に縮約を外して和を取り、本来の形に戻して、分配法則、定数\(L^{\mu}_{\ \nu}\)(慣性系の速度のみに依る)を微分の外に出す。丁寧にやる。 \[=L^{\mu}_{\ 0}\frac{d}{d\tau}x^{0}+L^{\mu}_{\ 1}\frac{d}{d\tau}x^{1}+L^{\mu}_{\ 2}\frac{d}{d\tau}x^{2}+L^{\mu}_{\ 3}\frac{d}{d\tau}x^{3}\] \[u'^{\mu}=L^{\mu}_{\ \nu}u^{\nu}\tag{4}\] ４元速度\(u^{\mu}\)は\(x^{\mu}\)と同じようにローレンツ変換できる。 次に４元運動量\(p^{\mu}\)を \[p^{\mu}:=mu^{\mu}\] で定義する。４元運動量のローレンツ変換は(4)式の両辺に\(m\)を掛けるだけなので、 \[p'^{\mu}=L^{\mu}_{\ \nu}p^{\nu}\tag{5}\] のようにローレンツ変換することができる。４元力を \[f^{\mu}:=\frac{dp^{\mu}}{d\tau}\] で定義する。４元力\(f^{\mu}\)のローレンツ変換は(5)式を\(\tau\)で微分することで、 \[f'^{\mu}=L^{\mu}_{\ \nu}f^{\nu}\] のようにローレンツ変換することができる。これで準備ができた。相対論的運動方程式は \[\frac{dp^{\mu}}{d\tau}=f^{\mu}\] のようにかける。 両辺をローレンツ変換すると、 \[L^{\mu}_{\ \nu}\frac{dp^{\nu}}{d\tau}=L^{\mu}_{\ \nu}f^{\nu}\] \[\frac{dL^{\mu}_{\ \nu}p^{\nu}}{d\tau}=L^{\mu}_{\ \nu}f^{\nu}\] \[\frac{dp'^{\mu}}{d\tau}=f'^{\mu}\] 運動方程式は４元運動量\(p^\mu\)の固有時\(\tau\)微分を４元力\(f^{\mu}\)とすることで、慣性系によらず運動方程式は同じ形で表せる。特殊相対性原理を満たす方程式である。

＊＊物理量のローレンツ変換＊＊

　ミンコフスキー空間上の位置\(x^\mu\mapsto x'^{\mu}=L^{\mu}_{\ \nu}x^{\nu}\)のようにローレンツ変換されるならば、ミンコフスキー空間の物理量\(A^{\mu}\)も、 \[A^\mu\mapsto A'^{\mu}=L^{\mu}_{\ \nu}A^{\nu}\] のようにローレンツ変換される。