今回から熱力学をやっていこうと思う。

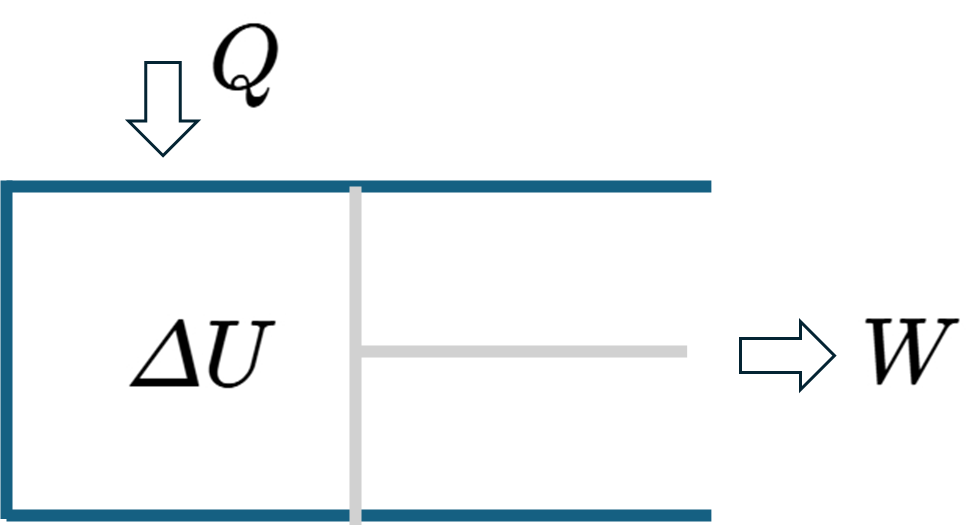
　熱力学第1法則はこの図に集約されている。理想気体が片側が開いた容器に入っている。理想気体が出ていかないようにピストンのようなものが付いている。この装置の外部から熱\(Q\)を加える。加えられた熱エネルギー\(Q\)は内部エネルギーの一部\(\varDelta U\)として蓄えられる、もしくは気体がする仕事\(W\)となる。 \[Q=\varDelta U+W\] という関係で表すことができる。これでおしまいと言えばそこまでなのだが、もう少し踏み込んでみよう。もう少し一般に熱力学第１法則は \[d'Q=dU+d'W\] のように表すことがある。\(d'Q\)は熱量の微小変化量、\(dU\)は内部エネルギーの微小変化量、\(d'W\)は仕事の微小変化量である。ここで気になるのは\(d'\)のダッシュが何なのかというところだろう。詳しく見ていこう。

理想気体の状態方程式は \[pV=nRT\] と表せる。気体の状態は温度\(T\)、体積\(V\)、圧力\(p\)の３つで決まっている。この３つのうち２つを決めることができれば残りの１つを状態方程式から決めることができる。状態方程式の\(n\)は気体の物質量である。\(R\)は気体定数である。物質量の定義は \[n:=\frac{N}{N_A}\] である。日常で状態方程式を扱う上で、気体分子の個数\(N\)は数がでかすぎるので、アボガドロ定数は約 \[N_A\simeq6.022\times 10^{23}\ \mathrm{mol^{-1}}\] で割ることで、扱いやすい数字の大きさにしているのである。ボルツマン定数 \[k_B:=\frac{R}{N}=1.380\ 649\times 10^{-23}\ \mathrm{JK^{-1}}\] を用いることで、理想気体の状態方程式は \[pV=\frac{N}{N_A}RT\] \[pV=Nk_BT\] となる。物質量の概念を経由せずに理想気体の方程式を圧力\(p\)、体積\(V\)、気体分子の個数\(N\)、温度\(T\)を使って表すことができる。こっちの方が個人的に好きなのでこの状態方程式を使うことにする。

一般に実在気体の内部エネルギー\(U\)は温度\(T\)と気体の体積\(V\)に依る量になっている。 \[U=U(T,V)\] なぜ体積依存の量になっているかというと、実在気体の分子には分子間力がある為である。別に\(U(T,V)\)でなくても\(U(T,p)\)などでも良いが、気体分子の熱運動の大きさを表す量である点から温度\(T\)と分子間力の直接の要因である体積\(V\)が自然な変数として選ばれている。内部エネルギーも状態量である。ここで本題に入る。 \[p,V,N,T,U\tag{1}\] \[Q,W\tag{2}\] 今物理量を(1)、(2)の２つの組に分けた。(1)が状態量で、(2)は状態量ではない。状態量とは読んでそのままの意味で、物質の状態あるのみから決めることのできる物理量である。

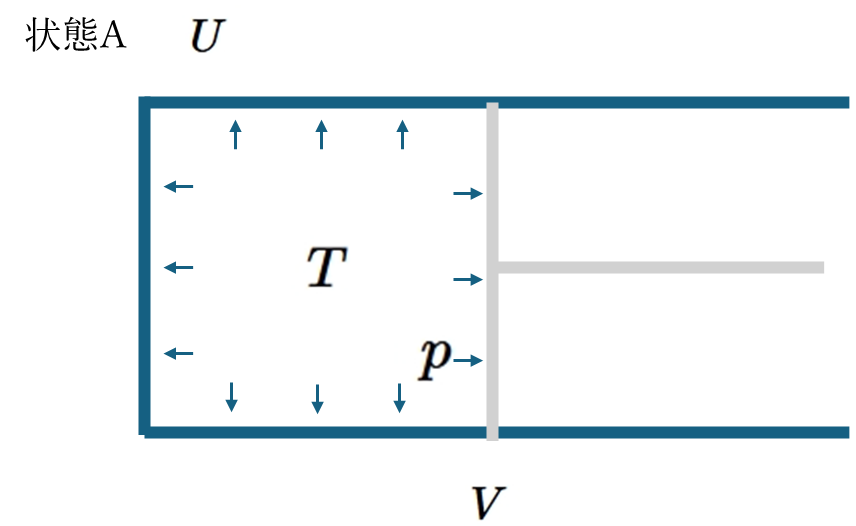
\(p,V,N,T,U\)はある状態Aを定めるだけで決めることができる量である。

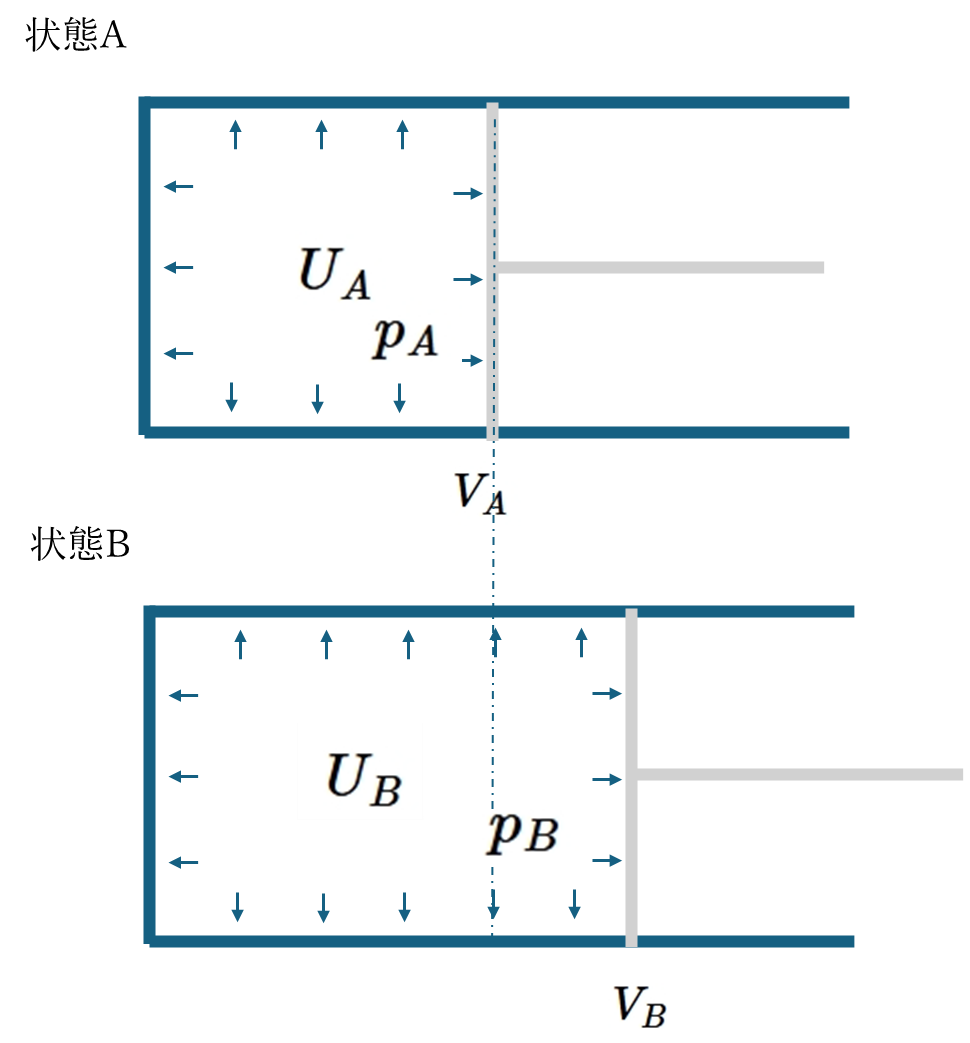
仕事の定義は、 \[W_{A\to B}:=\int_{V_A}^{V_B}pdV\] であるため熱量は熱力学第１法則から、 \[Q_{A\to B}=U_B-U_A+W_{A\to B}\] となる。仕事\(W\)や熱量\(Q\)は状態\(A\)から状態\(B\)にどのような仮定を経てたどり着いたのかが必要な量である。

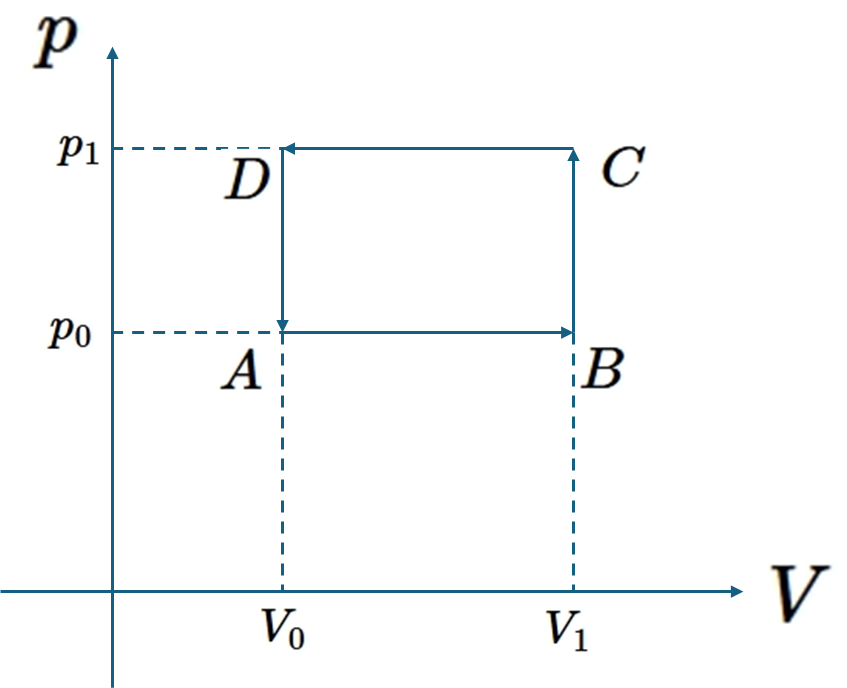
仕事、熱量の性質を見たいので、経路\(C_1=A\to B\to C\)と経路\(C_2=A\to D \to C\)の２つの経路で仕事がどのように表せるか見てみる。まずは\(C_1\)から、 \[W_{C_1}=W_{A\to B}+W_{B\to C}\] \[=\int_{V_0}^{V_1}p_0dV+\int_{V_1}^{V_1}pdV=p_0(V_1-V_0)+0\] \[W_{C_1}=p_0(V_1-V_0)\tag{3}\] 次に\(W_{C_2}\)を求める。 \[W_{C_2}=W_{A\to D}+W_{D\to C}\] \[\int_{V_0}^{V_0}pdV+\int_{V_0}^{V_1}p_1dV\] \[W_{C_2}=p_1(V_1-V_0)\tag{4}\] 仕事\(W\)微分を求めるため、 \[(p_1,V_1)\to (p,V)\] とする。 \[W_{C_1}=p_0(V-V_0)\] \[W_{C_2}=p(V-V_0)\] 仕事の偏微分を求めておく。 \[\frac{\partial W_{C_1}(p,V)}{\partial p}=0,\ \frac{\partial W_{C_1}(p,V)}{\partial V}=p_0\] \[\frac{\partial W_{C_2}(p,V)}{\partial p}=-(V-V_0),\ \frac{\partial W_{C_2}(p,V)}{\partial V}=p\] これを見てもらえば分かるように一般に \[dW=\frac{\partial W(p,V)}{\partial p}dp+\frac{\partial W(p,V)}{\partial V}dV\] となるような、 \[\frac{\partial W(p,V)}{\partial p},\ \frac{\partial W(p,V)}{\partial V}\] は無い。また \[\frac{\partial^2 W_{C_1}(p,V)}{\partial p\partial V}=0,\ \frac{\partial^2 W_{C_1}(p,V)}{\partial V\partial p}=0\] \[\frac{\partial^2 W_{C_2}(p,V)}{\partial p\partial V}=-1,\ \frac{\partial^2 W_{C_2}(p,V)}{\partial V\partial p}=1\] であるから、 \[\frac{\partial^2 W(p,V)}{\partial p\partial V}\neq\frac{\partial^2 W(p,V)}{\partial V\partial p}\] 偏微分の順番を変更することが出いない。仕事\(W\)は経路依存の量である。一方で理想気体の内部エネルギーは \[U(T,V)=\frac{3}{2}Nk_BT\] である。仕事と比較したいので、気体の状態方程式\(pV=Nk_BT\)を用いて内部エネルギーを\(U(p,V)\)で表示する \[U(p,V)=\frac{3}{2}pV\] 内部エネルギーの偏微分は \[\frac{\partial U(p,V)}{\partial p}=\frac{3}{2}V,\ \frac{\partial U(p,V)}{\partial V}=\frac{3}{2}p\] であり、内部エネルギーは全微分可能である。 \[dU(p,V)=\frac{3}{2}Vdp+\frac{3}{2}pdV\] また \[\frac{\partial^2 U(p,V)}{\partial p\partial V}=\frac{\partial U(p,V)}{\partial V\partial p}=\frac{3}{2}\] であるため偏微分の順序を交換することができる。全微分可能であるというのは良い性質があるある閉じた経路\(\Omega\)今回の例だと\(\Omega=A\to B\to C\to D\to A\)のように１周して戻ってくる経路において、 \[\oint_\Omega dU(p,V)=\int_{p_A}^{p_A}\frac{3}{2}Vdp+\int_{V_A}^{V_A}\frac{3}{2}pdV=0\] 経路積分が０になる、全微分できない仕事に付いては(3)(4)式の結果を用いて \[W_{\Omega}=W_{A \to B \to C}+W_{C \to D \to A}=p_0(V_1-V_0)-p_1(V_1-V_0)\] \[W_{\Omega}=(p_0-p_1)(V_1-V_0)\] となる。\(W\)全微分\(dW\)できないため、仕事の微小量を\(d'W\)や\(\delta W\)としている。熱量\(Q\)についても同様である。\(Q\)の１回微分は \[\frac{\partial Q(p,V)}{\partial p}=\frac{\partial (U(p,V)-U(p_0,V_0)+W(p,V))}{\partial p}=\frac{\partial U}{\partial p}+\frac{\partial W}{\partial p}\] \[\frac{\partial Q(p,V)}{\partial V}=\frac{\partial (U(p,V)-U(p_0,V_0)+W(p,V))}{\partial p}=\frac{\partial U}{\partial V}+\frac{\partial W}{\partial V}\] \(Q\)の２回微分は \[\frac{\partial^2 Q(p,V)}{\partial V\partial p}=\frac{\partial^2 U}{\partial V\partial p}+\frac{\partial^2 W}{\partial V\partial p}\] \[\frac{\partial^2 Q(p,V)}{\partial p\partial V}=\frac{\partial^2 U}{\partial p\partial V}+\frac{\partial^2 W}{\partial p\partial V}\] であるから、 \[\frac{\partial^2 Q(p,V)}{\partial V\partial p}\neq\frac{\partial^2 Q(p,V)}{\partial p\partial V}\] 熱量\(Q\)も前微分できないため\(d'Q\)などと書かれている。

　状態量\(p,V,N,T\)は状態方程式を使うことで、 \[p=p(V,N,T)\] \[V=V(p,N,T)\] \[N=N(p,V,T)\] \[T=T(p,V,N)\] などと表せるはずである。ある状態量\(f\)が\(x_1,x_2,x_3\)の変数で表せるとしよう。 \[df(x_1,x_2,x_3)=\frac{\partial f(x_1,x_2,x_3)}{\partial x_1}dx_1+\frac{\partial f(x_1,x_2,x_3)}{\partial x_2}dx_2+\frac{\partial f(x_1,x_2,x_3)}{\partial x_3}dx_3\] などと前微分できるはずなので、どの状態量でも内部エネルギーの時に示した性質が使える。